
���� ��1�������������������������ʾ�����ɵõ�����켣���̣�
��2����S��u��v��������D��u��0����W��u��$\frac{1}{2}$v�����ɴ��뷨�����ɵõ�����켣���̣�
��3����M��m��n����N��s��t����������Բ���̣��ɵ�������е�����깫ʽ��ֱ�ߵ�б�ʹ�ʽ�����ɵõ�����켣���̣�
��4�����ֱ�߷��̣�������Բ���̣�������OA��OBΪ�ڱߵ�ƽ���ı���OAEB���ɵ�$\overrightarrow{OE}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$�����������ļӷ��������㣬����ȥ���������ɵõ�����켣���̣�
��� �⣺��1����Բ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1��F1��-1��0����F2��1��0����
$\overrightarrow{T{F}_{1}}$•$\overrightarrow{T{F}_{2}}$=2x2+3���ɵã�-1-x����1-x��+y2=2x2+3��
����ɵ�y2-x2=4��
��2����S��u��v��������D��u��0����W��u��$\frac{1}{2}$v����
��x=u��y=$\frac{1}{2}$v����Ϊu=x��v=2y������Բ���̿ɵ�W�Ĺ켣����Ϊ$\frac{{x}^{2}}{4}$+$\frac{4{y}^{2}}{3}$=1��
��3����M��m��n����N��s��t��������
$\frac{{m}^{2}}{4}$+$\frac{{n}^{2}}{3}$=1��$\frac{{s}^{2}}{4}$+$\frac{{t}^{2}}{3}$=1��
��ʽ����ɵ�$\frac{��m-s����m+s��}{4}$+$\frac{��n-t����n+t��}{3}$=0��
��m+s=2��n+t=2��kMN=$\frac{n-t}{m-s}$���ɵ�kMN=-$\frac{3}{4}$��
��MN�е�Q�Ĺ켣����Ϊy-1=-$\frac{3}{4}$��x-1������Ϊy=-$\frac{3}{4}$x+$\frac{7}{4}$��
��4����P��3��0����ֱ��l��y=k��x-3����������Բ���̿ɵ�
��3+4k2��x2-24k2x+36k2-12=0��
�ɡ���0�ɵ�k2��$\frac{3}{5}$��
��A��x1��y1����B��x2��y2�����ɵ�x1+x2=$\frac{24{k}^{2}}{3+4{k}^{2}}$��
y1+y2=k��x1+x2-6��=$\frac{-18k}{3+4{k}^{2}}$��
����OA��OBΪ�ڱߵ�ƽ���ı���OAEB���ɵ�$\overrightarrow{OE}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$��
����x��y��=��x1+x2��y1+y2����
��Ϊ$\left\{\begin{array}{l}{x=\frac{24{k}^{2}}{3+4{k}^{2}}}\\{y=-\frac{18k}{3+4{k}^{2}}}\end{array}\right.$����ȥk���ɵ�3x2+4y2-18x=0��0��x��$\frac{8}{3}$����
���� ���⿼��켣���̵���ע������ֱ�ӷ������ʹ��뷨������ת�Ʒ����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
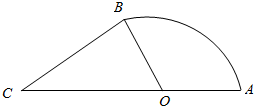 ��湫˾Ϊij���ֳ����ij����ʩ�������������ݸ���ʩ����ۣ���Ƴɵ�ƽ��ͼ�ɰ뾶Ϊ2m������AOB����������BCO���ɣ�����C��O��A��һ��ֱ���ϣ���ACB=$\frac{��}{4}$���Ǹ���ʩƽ��ͼ�����ΪS��x��m2����AOB=xrad������$\frac{��}{2}$��x���У�
��湫˾Ϊij���ֳ����ij����ʩ�������������ݸ���ʩ����ۣ���Ƴɵ�ƽ��ͼ�ɰ뾶Ϊ2m������AOB����������BCO���ɣ�����C��O��A��һ��ֱ���ϣ���ACB=$\frac{��}{4}$���Ǹ���ʩƽ��ͼ�����ΪS��x��m2����AOB=xrad������$\frac{��}{2}$��x���У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��y | B�� | x+y��0 | C�� | x��y | D�� | x2��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -sin2x | B�� | -2cosx | C�� | 2sinx | D�� | 2cosx |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com