练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】A在直角坐标系中,曲线的参数方程为,( 为参数),直线的方程为以为极点, 轴的正半轴为极轴建立极坐标系.

    （1）求曲线和直线的极坐标方程；

    （2）若直线与曲线交于两点，求

    已知不等式的解集为.

    （1）求的值；

    （2）若，求证：

    【答案】（1）见解析；（2）. （1）;（2）证明见解析.

    【解析】试题分析：A（1）先消参转化为普通方程，再利用普通方程与极坐标的转化公式转化为极坐标；（2）根据极坐标中的几何意义， 证明即可.B（1）分区间去绝对值号解不等式即可；（2）利用均值不等式证明.

    试题解析： （1）曲线的普通方程为,则的极坐标方程为,由于直线过原点,且倾斜角为,故其极坐标为 (或).

    （2）由,得,故

    （1）由,得或,解得

    （2）由（1）知

    当且仅当即时取等号, ,即

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了对某课题进行研究，用分层抽样方法从三所高校的相关人员中，抽取若干人组成研究小组，有关数据见下表（单位：人）

    高校

    相关人数

    抽取人数

    A

    18


    B

    36

    2

    C

    54


    （Ⅰ）求，；

    （Ⅱ）若从高校抽取的人中选2人作专题发言，求这二人都来自高校的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线： 的焦点为，过点的直线与相交于、两点，点关于轴的对称点为．

    （Ⅰ）判断点是否在直线上，并给出证明；

    （Ⅱ）设，求的内切圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为响应国家“精准扶贫，产业扶贫“的战略，进一步优化能源消费结构，某市决定在一地处山区的县推进光伏发电项目，在该县山区居民中随机抽取50户，统计其年用电量得到以下统计表，以样本的频率作为概率．

    用电量（度）

    户数

    5

    15

    10

    15

    5

    （1）在该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数为，求的数学期望；

    （2）已知该县某山区自然村有居民300户，若计划在该村安装总装机容量为300千瓦的光伏发电机组，该机组所发电量除保证该村正常用电外，剩余电量国家电网以元/度进行收购．经测算以每千瓦装机容量平均发电1000度，试估计该机组每年所发电量除保证正常用电外还能为该村创造直接收益多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正四棱锥中， ，侧棱与底面所成角的正切值为．

    （1）若是中点，求异面直线与所成角的正切值；

    （2）求侧面与底面所成二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,已知椭圆的长轴长是短轴长的倍，右焦点为,点分别是该椭圆的上、下顶点，点是直线上的一个动点（与轴交点除外），直线交椭圆于另一点，记直线, 的斜率分别为

    （1）当直线过点时，求的值；

    （2）求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）若，求曲线在处的切线方程；

    （2）若当时， ，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥中， 和是边长为的等边三角形， ， 是中点， 是中点．

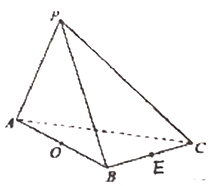
    （Ⅰ）求证：平面平面；

    （Ⅱ）求直线与平面所成角的正弦值的大小；

    （Ⅲ）在棱上是否存在一点，使得的余弦值为？若存在，指出点在上的位置；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中，△是等边三角形，△是等腰直角三角形，，平面平面，平面，点为的中点,连接.

    (1)求证：∥平面；

    (2)若，求三棱锥的体积.

    查看答案和解析>>

    同步练习册答案