
【题目】如图,在正方体![]() 中,E、F、G、H分别是棱
中,E、F、G、H分别是棱![]() 、
、![]() 、
、![]() 、
、![]() 的中点.
的中点.
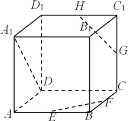
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
【答案】(1)直线![]() 与
与![]() 相交;详见解析(2)
相交;详见解析(2)![]()
【解析】
(1) 延长![]() 与
与![]() 必交于C右侧一点P,延长
必交于C右侧一点P,延长![]() 与
与![]() 必交于C右侧一点Q,证明P与Q重合,从而得到答案.
必交于C右侧一点Q,证明P与Q重合,从而得到答案.
(2)由![]() ,可得
,可得![]() ,则
,则![]() 与
与![]() 所成的角即为
所成的角即为![]() 与
与![]() 所成的角,然后在三角形中求解.
所成的角,然后在三角形中求解.
解:(1)取![]() 的中点
的中点![]()
∵E、F、I分别是正方形![]() 中
中![]() 、
、![]() 、
、![]() 的中点
的中点
∴![]()
∴在平面![]() 中,延长
中,延长![]() 与
与![]() 必交于C右侧一点P,且
必交于C右侧一点P,且![]()
同理,在平面![]() 中,延长
中,延长![]() 与
与![]() 必交于C右侧一点Q,且
必交于C右侧一点Q,且![]()
∴P与Q重合
进而,直线![]() 与
与![]() 相交
相交
方法二:∵在正方体![]() 中,E、H分别是
中,E、H分别是![]() 、
、![]() 的中点
的中点
∴![]()
∴![]() 是平行四边形
是平行四边形
∴![]()
又∵F、G分别是![]() 、
、![]() 的中点
的中点
∴![]()
∴![]() ,
,![]()
∴![]() 、
、![]() 是梯形
是梯形![]() 的两腰
的两腰
∴直线![]() 与
与![]() 相交
相交
(2)解:∵在正方体![]() 中,
中,![]()
∴![]() 是平行四边形
是平行四边形
∴![]()
又∵E、F分别是![]() 、
、![]() 的中点
的中点
∴![]()
∴![]()
∴![]() 与
与![]() 所成的角即为
所成的角即为![]() 与
与![]() 所成的角
所成的角
(或:![]() 与
与![]() 所成的角即为
所成的角即为![]() 及其补角中的较小角)①
及其补角中的较小角)①
又∵在正方体![]() 中,
中,![]() 为等边三角形
为等边三角形
∴![]() ②
②
∴由①②得直线![]() 与
与![]() 所成的角为
所成的角为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着互联网经济逐步被人们接受,网上购物的人群越来越多,网银交易额也逐年增加,某地连续五年的网银交易额统计表,如表所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网银交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,工作人员将上表的数据进行了处理,![]() ,
,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测2020年该地网银交易额.
(附:在线性回归方程![]() 中,
中,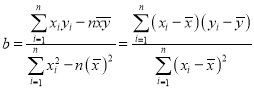 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的为![]()
A.已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是![]()
B.向量![]() ,
,![]() 不能作为平面内所有向量的一组基底
不能作为平面内所有向量的一组基底
C.若![]() ,则
,则![]() 在
在![]() 方向上的正射影的数量为
方向上的正射影的数量为![]()
D.三个不共线的向量![]() ,
,![]() ,
,![]() ,满足
,满足
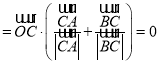 ,则
,则![]() 是
是![]() 的内心
的内心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会研究机构,为了研究大学生的阅读习惯,随机调查某大学40名不同性别的大学生在购买食物时是否读营养说明,其中男女各一半,男生中有![]() 表示会读,女生中有
表示会读,女生中有![]() 表示不会读.
表示不会读.
(1)根据调查结果,得到如下2╳2列联表:
男 | 女 | 总计 | |
读营养说明 | |||
不读营养说明 | |||
总计 |
(2)根据以上列联表,进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
P(K2≥k) | 0.10 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() 是边长为2的正三角形,顶点
是边长为2的正三角形,顶点![]() 在
在![]() 上的射影为点
上的射影为点![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年微信用户数量统计显示,微信注册用户数量已经突破
年微信用户数量统计显示,微信注册用户数量已经突破![]() 亿.微信用户平均年龄只有
亿.微信用户平均年龄只有![]() 岁,
岁, ![]() 的用户在
的用户在![]() 岁以下,
岁以下, ![]() 的用户在
的用户在![]() 岁之间,为调查大学生这个微信用户群体中每人拥有微信的数量,现在从北京大学生中随机抽取
岁之间,为调查大学生这个微信用户群体中每人拥有微信的数量,现在从北京大学生中随机抽取![]() 位同学进行了抽样调查,结果如下:
位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )若从
)若从![]() 位同学中随机抽取
位同学中随机抽取![]() 人,求这
人,求这![]() 人中恰有
人中恰有![]() 人微信群个数超过
人微信群个数超过![]() 个的概率.
个的概率.
(![]() )以这
)以这![]() 个人的样本数据估计北京市的总体数据且以频率估计概率,若从全市大学生中随机抽取
个人的样本数据估计北京市的总体数据且以频率估计概率,若从全市大学生中随机抽取![]() 人,记
人,记![]() 表示抽到的是微信群个数超过
表示抽到的是微信群个数超过![]() 个的人数,求
个的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与直线y=
与直线y=![]() x-2
x-2![]() 相切,设椭圆的上顶点为M,
相切,设椭圆的上顶点为M, ![]() 是椭圆的左右焦点,且⊿M
是椭圆的左右焦点,且⊿M![]() 为等腰直角三角形。(1)求椭圆的标准方程;(2)直线l过点N(0,-
为等腰直角三角形。(1)求椭圆的标准方程;(2)直线l过点N(0,-![]() )交椭圆于A,B两点,直线MA、MB分别与椭圆的短轴为直径的圆交于S,T两点,求证:O、S、T三点共线。
)交椭圆于A,B两点,直线MA、MB分别与椭圆的短轴为直径的圆交于S,T两点,求证:O、S、T三点共线。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com