
【题目】已知等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
【答案】(Ⅰ)an=![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)设出等比数列的公比q,由![]() ,利用等比数列的通项公式化简后得到关于q的方程,由已知等比数列的各项都为正数,得到满足题意q的值,然后再根据等比数列的通项公式化简
,利用等比数列的通项公式化简后得到关于q的方程,由已知等比数列的各项都为正数,得到满足题意q的值,然后再根据等比数列的通项公式化简![]() ,把求出的q的值代入即可求出等比数列的首项,根据首项和求出的公比q写出数列的通项公式即可;(Ⅱ)把(Ⅰ)求出数列{an}的通项公式代入设bn=log3a1+log3a2+…+log3an,利用对数的运算性质及等差数列的前n项和的公式化简后,即可得到bn的通项公式,求出倒数即为
,把求出的q的值代入即可求出等比数列的首项,根据首项和求出的公比q写出数列的通项公式即可;(Ⅱ)把(Ⅰ)求出数列{an}的通项公式代入设bn=log3a1+log3a2+…+log3an,利用对数的运算性质及等差数列的前n项和的公式化简后,即可得到bn的通项公式,求出倒数即为![]() 的通项公式,然后根据数列的通项公式列举出数列的各项,抵消后即可得到数列{
的通项公式,然后根据数列的通项公式列举出数列的各项,抵消后即可得到数列{![]() }的前n项和
}的前n项和
试题解析:(Ⅰ)设数列{an}的公比为q,由![]() =9a2a6得
=9a2a6得![]() =9
=9![]() ,所以q2=
,所以q2=![]() .
.
由条件可知q>0,故q=![]() .由2a1+3a2=1得2a1+3a1q=1,所以a1=
.由2a1+3a2=1得2a1+3a1q=1,所以a1=![]() .
.
故数列{an}的通项公式为an=![]() .
.
(Ⅱ)bn=log3a1+log3a2+…+log3an=-(1+2+…+n)=-![]() .
.
故![]() .
.
![]()
所以数列![]() 的前n项和为
的前n项和为![]()


科目:高中数学 来源: 题型:
【题目】围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2
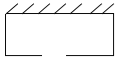
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2![]() 的进出口,如图所示,已知旧墙的维修费用为
的进出口,如图所示,已知旧墙的维修费用为![]() 元/
元/![]() ,新墙的造价为
,新墙的造价为![]() 元/
元/![]() ,设利用的旧墙的长度为
,设利用的旧墙的长度为![]() ,费用为
,费用为![]() 元.
元.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() 的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计资料,我国能源生产自1992年以来发展很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据:1992年8.6亿吨,5年后的1997年10.4亿吨,10年后的2002年12.9亿吨.有关专家预测,到2007年我国能源生产总量将达到17.1亿吨,则专家是依据下列哪一类函数作为数学模型进行预测的( )
A.一次函数 B.二次函数 C.指数函数 D.对数函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)=loga(2+x)-loga(2-x)(a>0且a≠1)
(Ⅰ)求f(x)定义域;
(Ⅱ)判断f(x)的奇偶性,并说明理由;
(Ⅲ)求使f(x)>0的x的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加夏令营的500名学生编号为:001,002,…,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的号码为003,这500名学生分住在三个营区,从001到200在第一营区,从201到355在第二营区,从356到500在第三营区,三个营区被抽中的人数分别为( )
A.20,15,15 B.20,16,14 C.12,14,16 D.21,15,14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是
A. 四边形确定一个平面
B. 经过一条直线和一个点确定一个平面
C. 经过三点确定一个平面
D. 两两相交且不共点的三条直线确定一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 每一点的横坐标保持不变,纵坐标变为原来的
每一点的横坐标保持不变,纵坐标变为原来的![]() 倍,得到曲线
倍,得到曲线![]() .
.
(1)写出![]() 的参数方程;
的参数方程;
(2)设直线![]() 与
与![]() 的交点为
的交点为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求:过线段
轴的正半轴为极轴建立极坐标系,求:过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com