分析:(1)椭圆
+y2=1中,由a=2,c=
,能求出椭圆离心率e
1,由双曲线与椭圆离心率之和为
,能求出双曲线的离心率e
2.
(2)由椭圆
+y2=1焦点为F
1(-
,0),F
2(
,0),双曲线与椭圆
+y2=1共焦点,知双曲线的焦点为F
1(-
,0),F
2(
,0),再由双曲线的离心率e
2=
.能求出双曲线的标准方程和渐近线方程.
(3)由
,得2x
2+4mx+4m
2-4=0,直线
l:y=x+m与椭圆有两个交点,知△=(4m)
2-8(4m
2-4)>0,由此能求出m的取值范围.
解答:解:(1)∵椭圆
+y2=1中,
a=2,c=
∴椭圆离心率e
1=
.
∵双曲线与椭圆
+y2=1的离心率之和为
,
∴双曲线的离心率e
2=
-=
.
(2)∵椭圆
+y2=1焦点为F
1(-
,0),F
2(
,0),
双曲线与椭圆
+y2=1共焦点,
∴双曲线的焦点为F
1(-
,0),F
2(
,0),
∵双曲线的离心率e
2=
.
∴双曲线的标准方程为
x2-=1,
∴双曲线的渐近线方程为y=
±x.
(3)由
,得2x
2+4mx+4m
2-4=0,
∵直线
l:y=x+m与椭圆有两个交点,
∴△=(4m)
2-8(4m
2-4)>0,
解得-
<m<.
故m的取值范围是(-
,).
点评:本题考查直线与圆锥曲线的位置关系的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.



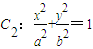 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.