
 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的分布列和数学期望;
的分布列和数学期望;科目:高中数学 来源:不详 题型:解答题
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 |  | 10 |  |
 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.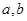 的值;
的值; :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率 ;(3)求
;(3)求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为摸出两球中白球的个数,
为摸出两球中白球的个数, 的期望.
的期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列及数学期望。
的分布列及数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 在R上不存在极值点的概率;
在R上不存在极值点的概率; ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com