
【题目】某公司为确定下一年投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年利润y(单位:万元)的影响,对近5年的宣传费xi和年利润yi(i=1,2,3,4,5)进行了统计,列出了下表:
x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程: ![]() =1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据
=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据 ![]() (yi﹣
(yi﹣ ![]() i)2=1.15) 参考公式:相关指数R2=1﹣
i)2=1.15) 参考公式:相关指数R2=1﹣ 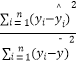
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ![]() =
= 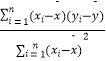 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x,参考数据:ln40=3.688,
x,参考数据:ln40=3.688, ![]() =538.
=538.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,如圆是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据:sin15°=0.2588,sin7.50=0.1305) 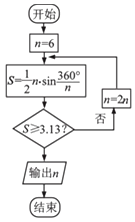
A.12
B.24
C.48
D.96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:直线mx﹣y+1=0与圆(x﹣2)2+y2=4有公共点;设命题q:实数m满足方程 ![]() +
+ ![]() =1表示双曲线.
=1表示双曲线.
(1)若“p∧q”为真命题,求实数m的取值范围;
(2)若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣lnx;g(x)= ![]() .
.
(1)讨论函数f(x)的单调性;
(2)求证:若a=e(e是自然常数),当x∈[1,e]时,f(x)≥e﹣g(x)恒成立;
(3)若h(x)=x2[1+g(x)],当a>1时,对于x1∈[1,e],x0∈[1,e],使f(x1)=h(x0),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界,已知函数
的上界,已知函数![]() .
.
(Ⅰ)若![]() 是奇函数,求
是奇函数,求![]() 的值.
的值.
(Ⅱ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,判断函数
上的值域,判断函数![]() 在
在![]() 上是否为有界函数,并说明理由.
上是否为有界函数,并说明理由.
(Ⅲ)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的函数,求实数
为上界的函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com