
| 解:(Ⅰ)∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB, BC 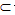 平面ABCD,而四边形ABCD为矩形 平面ABCD,而四边形ABCD为矩形∴BC⊥AB, ∴BC⊥平面ABEF ∵AF  平面ABEF 平面ABEF∴BC⊥AF, ∵BF⊥AF,BC∩BF=B, ∴AF⊥平面FBC; (Ⅱ)取FD中点N,连接MN、AN,则MN∥CD, 且MN= 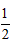 CD,又四边形ABCD为矩形, CD,又四边形ABCD为矩形,∴MN∥OA,且MN=OA, ∴四边形AOMN为平行四边形, ∴OM∥AN, 又∵OM 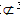 平面DAF,ON 平面DAF,ON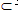 平面DAF 平面DAF∴OM∥平面DAF; (Ⅲ)过F作FG⊥AB与G, 由题意可得:FG⊥平面ABCD, ∴VF-ABCD = 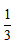 S矩形ABCD·FG= S矩形ABCD·FG= FG FG ∵CF⊥平面ABEF ∴VF-CBE=VC-BFE =  S△BFE·CB= S△BFE·CB= = =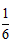 FG, FG,∴VF-ABCD∶VF-CBE=4∶ 1。 |
 |


科目:高中数学 来源: 题型:
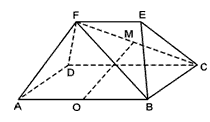
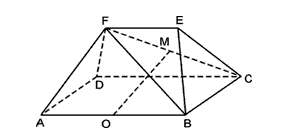
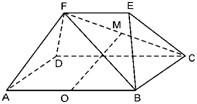 已知多面体ABCDFE中,四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1.
已知多面体ABCDFE中,四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1.查看答案和解析>>
科目:高中数学 来源: 题型:
已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD = EF = 1.
(Ⅰ)求证:AF⊥平面FBC;
 (Ⅱ)求证:OM∥平面DAF;
(Ⅱ)求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两
个锥体的体积分别为VF-ABCD,VF-CBE,求
VF-ABCD∶VF-CBE 的值.
![]()
|

|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年辽宁省本溪市普通高中模块数学试卷(必修2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com