
【题目】如图,某市园林局准备绿化一块直径为![]() 的半圆空地,
的半圆空地,![]() 以外的地方种草,
以外的地方种草,![]() 的内接正方形
的内接正方形![]() 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若![]() 为定值),
为定值),![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]()
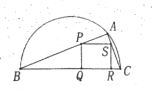
(1)用![]() 表示
表示![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 取得最大值,并求出此最大值.
取得最大值,并求出此最大值.
科目:高中数学 来源: 题型:
【题目】某棋类游戏的规则如下:棋子的初始位置在起点处,玩家每掷出一枚骰子,朝上一面的点数即为向终点方向前进的格子数,(比如玩家一开始掷出的骰子点数为3,则走到炸弹所在位置),若踩到炸弹则返回起点重新开始,若达到终点则游戏结束.现在已知小明掷完三次骰子后游戏恰好结束,则所有不同的情况种数为__________.
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂2万元设计了某款式的服装,根据经验,每生产1百套该款式服装的成本为1万元,每生产![]() (百套)的销售额(单位:万元)
(百套)的销售额(单位:万元)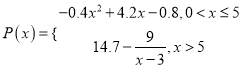 .
.
(1)若生产6百套此款服装,求该厂获得的利润;
(2)该厂至少生产多少套此款式服装才可以不亏本?
(3)试确定该厂生产多少套此款式服装可使利润最大,并求最大利润.(注:利润=销售额-成本,其中成本=设计费+生产成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
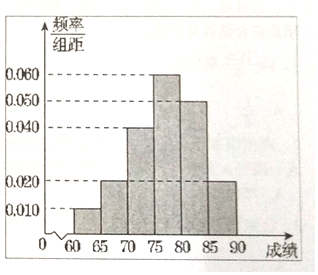
【题目】在某次综合素质测试中,共设有60个考场,每个考场30名考生,在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考场中座位号为06的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
问:
在这个调查采样中,采用的是什么抽样方法?
估计这次测试中优秀(80分及以上)的人数;
写出这60名考生成绩的众数、中位数、平均数的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】亳州某商场举行购物抽奖活动,规定每位顾客从装有编号为0,1,2,3四个相同小求的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6,则中一等奖;等于5中二等奖;等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求不中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数![]() 中定义一种新运算:
中定义一种新运算: ![]() ,对实数
,对实数![]() 经过运算
经过运算![]() 后是一个确定的唯一的实数。
后是一个确定的唯一的实数。![]() 运算有如下性质:(1)对任意实数
运算有如下性质:(1)对任意实数![]() ,
, ![]() ;(2)对任意实数
;(2)对任意实数![]() ,
, ![]() 那么:关于函数
那么:关于函数![]() 的性质下列说法正确的是:①函数
的性质下列说法正确的是:①函数![]() 的最小值为3;②函数
的最小值为3;②函数![]() 是偶函数;③函数
是偶函数;③函数![]() 在
在![]() 上为减函数,这三种说法正确的有__________.
上为减函数,这三种说法正确的有__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com