【题目】在空间中，给出下列说法：①平行于同一个平面的两条直线是平行直线；②垂直于同一条直线的两个平面是平行平面；③若平面
内有不共线的三点到平面
的距离相等，则
；④过平面的一条斜线，有且只有一个平面与平面垂直.其中正确的是（ ）
A. ①③B. ②④C. ①④D. ②③
备战中考寒假系列答案科目：高中数学 来源： 题型：
【题目】已知数列
满足
（
，且
），且
，设
，，数列
满足
.
（1）求证：数列
是等比数列并求出数列的通项公式；
（2）求数列的前n项和
；
（3）对于任意，
，
恒成立，求实数m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C：y2=2px（p＞0）过点M（m，2），其焦点为F，且|MF|=2．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设E为y轴上异于原点的任意一点，过点E作不经过原点的两条直线分别与抛物线C和圆F：（x﹣1）2+y2=1相切，切点分别为A，B，求证：直线AB过定点F（1，0）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四棱锥P－ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点．
(Ⅰ)求证：PC∥平面EBD；
(Ⅱ)求证：平面PBC⊥平面PCD.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲乙两地生产某种产品，他们可以调出的数量分别为300吨、750吨.A，B，C三地需要该产品数量分别为200吨，450吨，400吨，甲地运往A，B，C三地的费用分别为6元/吨、3元/吨，5元/吨，乙地运往A，B，C三地的费用分别为5元/吨，9元/吨，6元/吨，问怎样调运，才能使总运费最小？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】东莞市公交公司为了方便广大市民出行，科学规划公交车辆的投放，计划在某个人员密集流动地段增设一个起点站，为了研究车辆发车的间隔时间
与乘客等候人数
之间的关系，选取一天中的六个不同的时段进行抽样调查，经过统计得到如下数据：
间隔时间（ | 8 | 10 | 12 | 14 | 16 | 18 |
等候人数（ | 16 | 19 | 23 | 26 | 29 | 33 |
调查小组先从这6组数据中选取其中的4组数据求得线性回归方程，再用剩下的2组数据进行检验，检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数
，再求与实际等候人数的差，若两组差值的绝对值均不超过1，则称所求的回归方程是“理想回归方程”.
参考公式：用最小二乘法求线性回归方程
的系数公式：
，
（1）若选取的是前4组数据，求关于的线性回归方程
；
（2）判断（1）中的方程是否是“理想回归方程”：
（3）为了使等候的乘客不超过38人，试用（1）中方程估计间隔时间最多可以设置为多少分钟？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地随着经济的发展，居民收入逐年增长，如表是该地一建设银行连续五年的储蓄存款（年底余额），如表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便，工作人员将上表的数据进行了处理，
得到表2：
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（1）求z关于t的线性回归方程；
（2）通过（1）中的方程，求出y关于x的回归方程；
（3）用所求回归方程预测到2010年年底，该地储蓄存款额可达多少？
附：对于线性回归方程
，
其中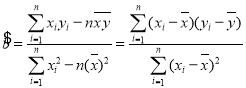
, 
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
