
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)设函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,若函数
,若函数![]() 是
是![]() 上的单调增函数,求
上的单调增函数,求![]() 的值;
的值;
(3)是否存在一条直线与函数![]() 的图象相切于两个不同的点?并说明理由.
的图象相切于两个不同的点?并说明理由.
【答案】(1)![]() 的极大值为
的极大值为![]() ;极小值为
;极小值为![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)![]() ,列极值表,即可求得
,列极值表,即可求得![]() 的极值;(2)设切线方程为
的极值;(2)设切线方程为![]() ,从而
,从而![]() ,记
,记![]() ,即求
,即求![]() 在
在![]() 上恒成立,将
上恒成立,将![]() 变形为
变形为![]() 恒成立,由基本不等式成立求得
恒成立,由基本不等式成立求得![]() ;(3)假设存在一条直线与函数
;(3)假设存在一条直线与函数![]() 的图象有两个不同的切点
的图象有两个不同的切点![]() ,
,![]() 分别写出
分别写出![]()
![]() 处的切线方程
处的切线方程![]() ,由
,由![]() 为同一直线得
为同一直线得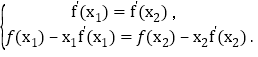 整理得
整理得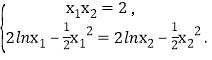 消去
消去![]() 得,
得,![]() ,令
,令![]() 构造函数
构造函数![]() ,求导求得
,求导求得![]() ,推出矛盾,说明假设不成立,则不存在
,推出矛盾,说明假设不成立,则不存在
(1) 当![]() 时,函数
时,函数![]() 的定义域为
的定义域为![]() .
.
则![]() ,令
,令![]()
![]() 得,
得,![]() 或
或![]() .列表:
.列表:
|
| 1 |
| 2 |
|
| + | 0 | 0 | + | |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以函数![]() 的极大值为
的极大值为![]() ;极小值为
;极小值为![]() .
.
(2)依题意,切线方程为![]() ,
,
从而![]() ,
,
记![]() ,
,
则![]() 在
在![]() 上为单调增函数,
上为单调增函数,
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
变形得![]() 在
在![]() 上恒成立 ,
上恒成立 ,
因为![]() (当且仅当
(当且仅当![]() 时,等号成立),
时,等号成立),
所以![]() ,从而
,从而![]() ,所以
,所以![]() .
.
(3)假设存在一条直线与函数![]() 的图象有两个不同的切点
的图象有两个不同的切点![]() ,
,![]() ,不妨
,不妨![]() ,则
,则![]() 处切线
处切线![]() 的方程为:
的方程为:![]() ,
,
![]() 处切线
处切线![]() 的方程为:
的方程为:![]() .
.
因为![]() ,
,![]() 为同一直线,所以
为同一直线,所以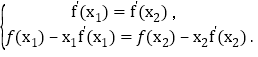 即
即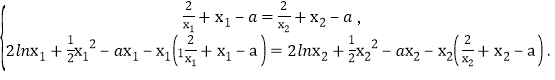
整理得,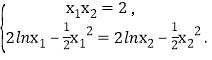 消去
消去![]() 得,
得,![]() .
.![]()
令![]() ,由
,由![]() 与
与![]() ,得
,得![]() ,
,
记![]() ,则
,则![]() ,
,
所以![]() 为
为![]() 上的单调减函数,所以
上的单调减函数,所以![]() .
.
从而![]() 式不可能成立,所以假设不成立,从而不存在一条直线与函数
式不可能成立,所以假设不成立,从而不存在一条直线与函数![]() 的图象有两个不同的切点.
的图象有两个不同的切点.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2![]() +sinB·cos2
+sinB·cos2![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“日行一万步,健康你一生”的养生观念已经深入人心,由于研究性学习的需要,某大学生收集了手机“微信运动”团队中特定甲、乙两个班级![]() 名成员一天行走的步数,然后采用分层抽样的方法按照
名成员一天行走的步数,然后采用分层抽样的方法按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分层抽取了20名成员的步数,并绘制了如下尚不完整的茎叶图(单位:千步):
分层抽取了20名成员的步数,并绘制了如下尚不完整的茎叶图(单位:千步):

已知甲、乙两班行走步数的平均值都是44千步.
(1)求![]() 的值;
的值;
(2)(ⅰ)若![]() ,求甲、乙两个班级100名成员中行走步数在
,求甲、乙两个班级100名成员中行走步数在![]() ,
, ![]() ,
, ![]() ,
, ![]() 各层的人数;
各层的人数;
(ⅱ)若估计该团队中一天行走步数少于40千步的人数比处于![]() 千步的人数少12人,求
千步的人数少12人,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 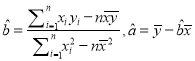 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,双曲线
,双曲线![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 的直线与抛物线在第一象限的交点为
的直线与抛物线在第一象限的交点为![]() ,且抛物线在点
,且抛物线在点![]() 处的切线与直线
处的切线与直线![]() 垂直,则
垂直,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com