
【题目】某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( ) 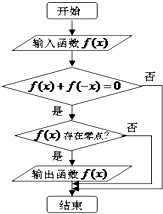
A.f(x)=x2
B.f(x)=sinx
C.f(x)=ex
D.f(x)= ![]()
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点. 
(1)求异面直线AB与EF所成角的余弦值;
(2)求E到平面ACD的距离;
(3)求EF与平面ACD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωxcosωx﹣cos2ωx﹣
sinωxcosωx﹣cos2ωx﹣ ![]() (ω>0,x∈R)的图象上相邻两个最高点的距离为π.
(ω>0,x∈R)的图象上相邻两个最高点的距离为π.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若△ABC三个内角A、B、C的对边分别为a、b、c,且c= ![]() ,f(C)=0,sinB=3sinA,求a,b的值.
,f(C)=0,sinB=3sinA,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支球队进行总决赛,比赛采用五场三胜制,即若有一队先胜三场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为二分之一.据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
(1)求总决赛中获得门票总收入恰好为150万元且甲获得总冠军的概率;
(2)设总决赛中获得的门票总收入为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若图所示,将若干个点摆成三角形图案,每条边(包括两个端点)n(n>1,n∈N*)个点,相应的图案中总的点数记为an , 则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() = .
= . 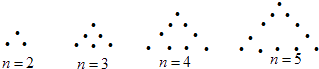
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ ![]() ax2﹣2bx
ax2﹣2bx
(1)设点a=﹣3,b=1,求f(x)的最大值;
(2)当a=0,b=﹣ ![]() 时,方程2mf(x)=x2有唯一实数解,求正数m的取值范围.
时,方程2mf(x)=x2有唯一实数解,求正数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果关于x的方程 ![]() 正实数解有且仅有一个,那么实数a的取值范围为( )
正实数解有且仅有一个,那么实数a的取值范围为( )
A.{a|a≤0}
B.{a|a≤0或a=2}
C.{a|a≥0}
D.{a|a≥0或a=﹣2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx﹣sinωx,sinωx),
=(cosωx﹣sinωx,sinωx), ![]() =(﹣cosωx﹣sinωx,2
=(﹣cosωx﹣sinωx,2 ![]() cosωx),设函数f(x)=
cosωx),设函数f(x)= ![]()
![]() +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ![]() ,1)
,1)
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ![]() ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com