分析:(Ⅰ)根据C,C
1分别是AB,A
1B
1的中点,则CC
1⊥BC,CC
1⊥AC,∠ACB是二面角A
1-CC
1-B的平面角,从而BC⊥AC,所以CA,CB,CC
1两两垂直,以点C为原点,分别以CA,CB,CC
1为x,y,z轴,建立空间直角坐标系,然后求出平面A
1BE的法向量为n和向量
,根据向量
与平面A
1BE的法向量垂直可知C
1D∥平面A
1BE.
(Ⅱ)先求出平面AA
1B
1B的法向量为m,根据平面A
1BE的法向量为n与法向量为m垂直,从而证得平面A
1BE⊥平面AA
1B
1B.
(Ⅲ)先求出向量
,设直线BC
1与平面A
1BE所成角为θ,则
sinθ=|cos<n,>|=||,从而求出所求.
解答: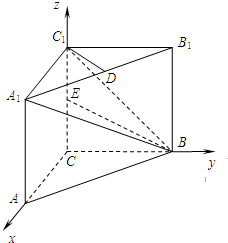
(Ⅰ)证明:由已知,将长方形AA
1B
1B沿CC
1对折后,二面角A
1-CC
1-B为直二面角,因为在长方形AA
1B
1B中,C,C
1分别是AB,A
1B
1的中点,所以CC
1⊥BC,CC
1⊥AC.即∠ACB是二面角A
1-CC
1-B的平面角.
所以∠ACB=90°.所以BC⊥AC.
所以CA,CB,CC
1两两垂直.
以点C为原点,分别以CA,CB,CC
1为x,y,z轴,建立空间直角坐标系.…(1分)
因为AB=2AA
1=4,且D,E分别是A
1B
1,CC
1的中点,
所以C
1(0,0,2),D(1,1,2),A
1(2,0,2),B(0,2,0),E(0,0,1).…(2分)
所以
=(1,1,0),
=(-2,2,-2),=(0,-2,1).
设平面A
1BE的法向量为n=(x,y,z),
所以
所以
令y=1,则z=2,x=-1.
所以n=(-1,1,2).…(3分)
又因为
•n=(1,1,0)•(-1,1,2)=0.
所以
⊥n.
又因为C
1D?平面A
1BE,
所以C
1D∥平面A
1BE.…(4分)
(Ⅱ)证明:由(Ⅰ)知A(2,0,0),A
1(2,0,2),B(0,2,0),
=(0,0,2),
=(-2,2,0).
设平面AA
1B
1B的法向量为m=(x,y,z),
所以
所以
令y=1,则x=1,z=0,所以m=(1,1,0).…(6分)
由(Ⅰ)知,平面A
1BE的法向量为n=(-1,1,2).
所以m•n=(1,1,0)•(-1,1,2)=0.
所以m⊥n.所以平面A
1BE⊥平面AA
1B
1B.…(8分)
(Ⅲ)解:由(Ⅰ)知,B(0,2,0),C
1(0,0,2).所以
=(0,-2,2).
又由(Ⅰ)知,平面A
1BE的法向量为n=(-1,1,2).…(10分)
设直线BC
1与平面A
1BE所成角为θ,则
sinθ=|cos<n, >|=||=||=.
所以直线BC
1与平面A
1BE所成角的正弦值为
.…(13分)
点评:本题主要考查了利用空间向量证明线面平行,面面垂直和线面所成角的度量,同时考查了推理论证的能力和计算能力,属于中档题.


 (Ⅰ)证明:由已知,将长方形AA1B1B沿CC1对折后,二面角A1-CC1-B为直二面角,因为在长方形AA1B1B中,C,C1分别是AB,A1B1的中点,所以CC1⊥BC,CC1⊥AC.即∠ACB是二面角A1-CC1-B的平面角.
(Ⅰ)证明:由已知,将长方形AA1B1B沿CC1对折后,二面角A1-CC1-B为直二面角,因为在长方形AA1B1B中,C,C1分别是AB,A1B1的中点,所以CC1⊥BC,CC1⊥AC.即∠ACB是二面角A1-CC1-B的平面角.

