
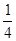 (3)
(3)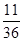
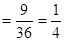 .
.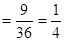 9分
9分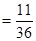 14分
14分

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
 小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过 克的概率.
克的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
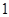 ,
,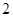 ,
,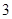 ,
,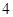 ,
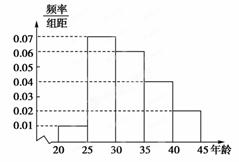
,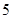 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下: | 等级 | 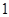 | 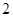 | 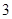 | 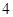 | 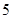 |
| 频率 | 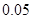 | 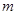 | 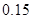 | 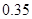 | 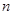 |
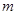 ,
,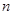 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 和p.
和p. ,求p的值;
,求p的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
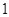 小时收费
小时收费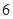 元,超过
元,超过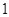 小时的部分每小时收费
小时的部分每小时收费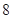 元(不足
元(不足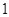 小时的部分按
小时的部分按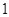 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过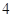 小时.
小时.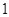 小时以上且不超过
小时以上且不超过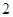 小时的概率为
小时的概率为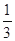 ,停车付费多于
,停车付费多于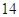 元的概率为
元的概率为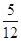 ,求甲停车付费恰为
,求甲停车付费恰为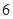 元的概率;
元的概率; 元的概率.
元的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com