
【题目】椭圆![]() 的中心在坐标原点,焦点
的中心在坐标原点,焦点![]() 在
在![]() 轴上,过坐标原点的直线
轴上,过坐标原点的直线![]() 交
交![]() 于
于![]() 两点,
两点,![]() ,
,![]() 面积的最大值为
面积的最大值为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆上与
是椭圆上与![]() 不重合的一点,证明:直线
不重合的一点,证明:直线![]() 的斜率之积为定值;
的斜率之积为定值;
(3)当点![]() 在第一象限时,
在第一象限时,![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)根据![]() 求出a,根据面积关系求出b;
求出a,根据面积关系求出b;
(2)设出点![]() 与
与![]() 的坐标,满足椭圆方程,计算两个斜率之积即可得到定值;
的坐标,满足椭圆方程,计算两个斜率之积即可得到定值;
(3)先证明![]() 是直角三角形,用直角边乘积的一半表示面积,结合基本不等式或勾型函数求面积最值.
是直角三角形,用直角边乘积的一半表示面积,结合基本不等式或勾型函数求面积最值.
(1)由题可设椭圆的方程![]() ,
,
![]() ,
,![]() ,
,
设![]() ,
,
![]() 面积
面积![]() ,
,
最大值为2,即![]() ,解得
,解得![]() ,
,
所以椭圆的方程为:![]() ;
;
(2)设![]() 是椭圆上与
是椭圆上与![]() 不重合的一点,
不重合的一点,
![]() ,
,![]() ,两式作差:
,两式作差:![]() ,
,
即:![]()
则直线![]() 的斜率之积
的斜率之积![]() ,
,
所以直线![]() 的斜率之积为定值;
的斜率之积为定值;
(3)点![]() 在第一象限,
在第一象限,![]() ,设直线
,设直线![]() 的方程
的方程![]() ,
,
由 得:
得:![]() ,
,
得![]() ,
,![]() ,
,
直线![]() 的斜率
的斜率![]() ,其方程为
,其方程为![]() ,
,
由 得:
得:![]()
设![]() ,则
,则![]() 是方程的两个根,由韦达定理:
是方程的两个根,由韦达定理:
![]() ,
,![]()
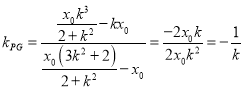 ,即
,即![]() ,
,
所以![]() ,
,
所以![]() 的面积
的面积
![]()



 ,设
,设![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
 ,
,
根据勾型函数性质:函数![]() 单调递增,
单调递增,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
 取得最大值
取得最大值![]() ,
,
即当![]() 时,
时,![]() 的面积取最大值
的面积取最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cos2B+cosB=1-cosAcosC.
(1)求证:a,b,c成等比数列;
(2)若b=2,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,公比q>0,S2=2a2-2,S3=a4-2,数列{an}满足a2=4b1,nbn+1-(n+1)bn=n2+n,(n∈N*).
(1)求数列{an}的通项公式;
(2)证明数列{![]() }为等差数列;
}为等差数列;
(3)设数列{cn}的通项公式为:Cn=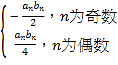 ,其前n项和为Tn,求T2n.
,其前n项和为Tn,求T2n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,
中,![]() ,
,![]() .令
.令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)是否存在正整数![]() ,(
,(![]()
![]() ),使得
),使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的![]() ,
,![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形, ![]() .
.

(Ⅰ)若![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 与平面
与平面![]() 所成角.
所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命. 为了研究司机开车时使用手机的情况,交警部门调查了![]() 名机动车司机,得到以下统计:在
名机动车司机,得到以下统计:在![]() 名男性司机中,开车时使用手机的有
名男性司机中,开车时使用手机的有![]() 人,开车时不使用手机的有
人,开车时不使用手机的有![]() 人;在
人;在![]() 名女性司机中,开车时使用手机的有
名女性司机中,开车时使用手机的有![]() 人,开车时不使用手机的有
人,开车时不使用手机的有![]() 人.
人.
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为开车时使用手机与司机的性别有关;
的把握认为开车时使用手机与司机的性别有关;
开车时使用手机 | 开车时不使用手机 | 合计 | |
男性司机人数 | |||
女性司机人数 | |||
合计 |
(2)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为![]() ,若每次抽检的结果都相互独立,求
,若每次抽检的结果都相互独立,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式与数据:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式
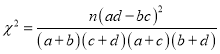 span>,其中
span>,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在直角梯形ABCD中,AD=1,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图②所示的几何体.
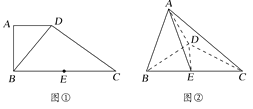
(1)求证:AB⊥平面ADC;
(2)若AC与平面ABD所成角的正切值为![]() ,求二面角B—AD—E的余弦值。
,求二面角B—AD—E的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 分别为椭圆
分别为椭圆![]() :
:![]() 的左右焦点,已知椭圆
的左右焦点,已知椭圆![]() 上的点
上的点![]() 到焦点
到焦点![]() ,
,![]() 的距离之和为4.
的距离之和为4.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,连结
,连结![]() 并延长交椭圆于点
并延长交椭圆于点![]() (
(![]() 为坐标原点),若
为坐标原点),若![]() ,
,![]() ,
,![]() 等比数列,求线段
等比数列,求线段![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 由曲线
由曲线![]() 和曲线
和曲线![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点.
所在圆锥曲线的焦点.
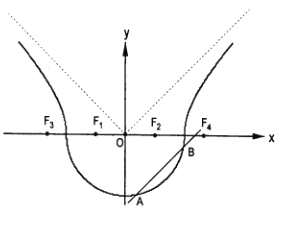
(1)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点
于点![]() ,求证:弦
,求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐近线上;
的另一条渐近线上;
(3)对于(1)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com