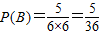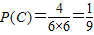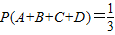同时掷两个骰子,
(1)指出点数的和是3的倍数的各种情形,并判断是否为互斥事件;
(2)求点数的和是3的倍数的概率.
【答案】
分析:(1)点数的和为3的倍数分,点数和为3,6,9,12,分别记为事件A、B、C、D事件都是彼此互斥的;
(2)本题是一个等可能事件的概率,分别做出等可能事件的概率,再根据互斥事件的概率做出要求的点数的和是3的倍数的概率.
解答:解:(1)点数的和为3的倍数分,点数和为3,6,9,12,
分别记为事件A、B、C、D事件都是彼此互斥的;
(2)由题意知本题是一个等可能事件的概率,
事件A中:3=1+2=2+1,∴P(A)=
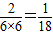
,
事件B中,6=1+5=2+4=3+3=4+2=5+1,共5种基本事件,∴
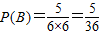
事件C中,9=3+6=4+5=5+4=6+3,共4种基本事件∴
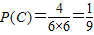
事件D中,12=6+6,1种基本事件,∴

总之:
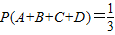 点评:
点评:本题考查随机事件和等可能事件的概率,本题解题的关键是看出事件包含四部分,这几部分之间是互斥关系.

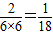 ,
,