
分析 (1)设事件A表示“取出的4支球拍上的数字互不相同”,则P(A)=1-P($\overline{A}$)=1-$\frac{{∁}_{5}^{1}•{∁}_{2}^{2}•{∁}_{8}^{2}}{{∁}_{10}^{4}}$.
(2)由题意可得ξ=2,3,4,5.则P(ξ=2)=$\frac{{∁}_{2}^{2}•{∁}_{2}^{2}}{{∁}_{10}^{4}}$.P(ξ=3)=$\frac{{∁}_{2}^{2}•{∁}_{4}^{2}+{∁}_{2}^{1}•{∁}_{4}^{3}}{{∁}_{10}^{4}}$,P(ξ=4)=$\frac{{∁}_{2}^{2}•{∁}_{6}^{2}+{∁}_{2}^{1}•{∁}_{6}^{3}}{{∁}_{10}^{4}}$,P(ξ=5)=$\frac{{∁}_{2}^{2}•{∁}_{8}^{2}+{∁}_{2}^{1}•{∁}_{8}^{3}}{{∁}_{10}^{4}}$.
解答 解:(1)设事件A表示“取出的4支球拍上的数字互不相同”,则P(A)=1-P($\overline{A}$)=1-$\frac{{∁}_{5}^{1}•{∁}_{2}^{2}•{∁}_{8}^{2}}{{∁}_{10}^{4}}$=$\frac{1}{3}$.
(2)由题意可得ξ=2,3,4,5.则P(ξ=2)=$\frac{{∁}_{2}^{2}•{∁}_{2}^{2}}{{∁}_{10}^{4}}$=$\frac{1}{210}$.
P(ξ=3)=$\frac{{∁}_{2}^{2}•{∁}_{4}^{2}+{∁}_{2}^{1}•{∁}_{4}^{3}}{{∁}_{10}^{4}}$=$\frac{14}{210}$,
P(ξ=4)=$\frac{{∁}_{2}^{2}•{∁}_{6}^{2}+{∁}_{2}^{1}•{∁}_{6}^{3}}{{∁}_{10}^{4}}$=$\frac{55}{210}$,
P(ξ=5)=$\frac{{∁}_{2}^{2}•{∁}_{8}^{2}+{∁}_{2}^{1}•{∁}_{8}^{3}}{{∁}_{10}^{4}}$=$\frac{140}{210}$.
∴ξ的分布列为:
| ξ | 2 | 3 | 4 | 5 |
| P | $\frac{1}{210}$ | $\frac{14}{210}$ | $\frac{55}{210}$ | $\frac{140}{210}$ |
点评 本题考查了相互独立事件与出事件的概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{4\sqrt{2}-\sqrt{6}}{2}$ | D. | 2$\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一种 | B. | 第二种 | C. | 两种一样 | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
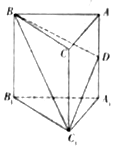 如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=8,D是AA1的中点
如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=8,D是AA1的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {1,2,4,5} | C. | {2,5} | D. | {0,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
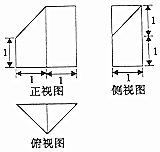
| A. | $\frac{9}{2}$+4$\sqrt{2}$ | B. | 5$+4\sqrt{2}$ | C. | 6$+4\sqrt{2}$ | D. | $\frac{13}{2}$$+4\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com