
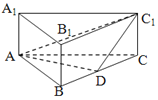
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() 是
是![]() 中点.
中点.
![]() 证明:
证明:![]() 平面
平面![]() ;
;
![]() 线段
线段![]() 上是否存在点
上是否存在点![]() ,使三棱锥
,使三棱锥![]() 的体积为
的体积为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(1)证明见解析;(2)![]() 为
为![]() 的中点.
的中点.
【解析】
![]() 连接
连接![]() ,与
,与![]() 交于点O,连接OD,
交于点O,连接OD,![]() ,由三角形中位线定理可得
,由三角形中位线定理可得![]() ,再由线面平行的判定可得
,再由线面平行的判定可得![]() 平面
平面![]() ;
;
![]() 连接
连接![]() ,假设线段
,假设线段![]() 上存在点N,使得三棱锥
上存在点N,使得三棱锥![]() 的体积为
的体积为![]() ,设N到平面
,设N到平面![]() 的距离为h,由三棱锥
的距离为h,由三棱锥![]() 的体积为
的体积为![]() 求得h,进一步求得
求得h,进一步求得
N为![]() 的中点得结论.
的中点得结论.
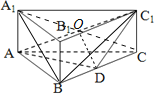
![]() 证明:如图,连接
证明:如图,连接![]() ,与
,与![]() 交于点O,连接OD,
交于点O,连接OD,![]() ,
,
在![]() 中,O和D分别是
中,O和D分别是![]() 和CB的中点,则
和CB的中点,则![]() ,
,
又![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ;
;
![]() 解:连接
解:连接![]() ,假设线段
,假设线段![]() 上存在点N,使得三棱锥
上存在点N,使得三棱锥![]() 的体积为
的体积为![]() ,
,
设N到平面![]() 的距离为h,
的距离为h,
由题意可知,![]() 为等边三角形,
为等边三角形,
又D为BC的中点,![]() .
.
又三棱柱![]() 为直三棱柱,
为直三棱柱,![]() ,
,
故AD![]() 平面
平面![]() ,
,
![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,
,
![]() 的面积为
的面积为![]() ,由三棱锥的体积公式可知,
,由三棱锥的体积公式可知,![]() ,
,
![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
故点N到平面![]() 的距离与点N到直线
的距离与点N到直线![]() 的距离相等,
的距离相等,
又![]() 为等腰直角三角形,
为等腰直角三角形,![]() 点C到直线
点C到直线![]() 的距离为
的距离为![]() .
.
又点B与点C到到平面![]() 的距离相等,故点B到直线
的距离相等,故点B到直线![]() 的距离也为
的距离也为![]() ,
,
![]() 当N为
当N为![]() 的中点时,点N到平面
的中点时,点N到平面![]() 的距离为
的距离为![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且点
两点,且点![]() 在第二象限.
在第二象限.![]() 与
与![]() 延长线交于点
延长线交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的3倍,求
面积的3倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且经过点
,且经过点![]() .
.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 过点
过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的任一条直线
的任一条直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( )
①命题“函数![]() 的最小值不为
的最小值不为![]() ”是假命题;
”是假命题;
②“![]() ”是“
”是“![]() ”的必要不充分条件;③若
”的必要不充分条件;③若![]() 为假命题,则
为假命题,则![]() ,
, ![]() 均为假命题;
均为假命题;
④若命题![]() :
: ![]() ,
, ![]() ,则
,则![]() :
: ![]() ,
, ![]() ;
;
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之.”翻译成现代语言如下:第一步,任意给定两个正整数,判断它们是否都是偶数,若是,用2约简;若不是,执行第二步:第二步,以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数,继续这个操作,知道所得的数相等为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数.现给出更相减损术的程序图如图所示,如果输入的![]() ,
,![]() ,则输出的
,则输出的![]() 为( ).
为( ).
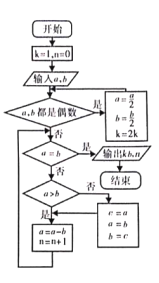
A. 3B. 6C. 7D. 8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ).在以
).在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() ;当
;当![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的值.
的值.
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com