
【题目】以下命题正确的是( )
A. 若直线![]() ,
,![]() ,
,![]() ,则直线a,b异面
,则直线a,b异面
B. 空间内任意三点可以确定一个平面
C. 空间四点共面,则其中必有三点共线
D. 直线![]() ,
,![]() ,
,![]() ,则直线a,b异面
,则直线a,b异面
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“既要金山银山,又要绿水青山”。某风景区在一个直径![]() 为
为![]() 米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点
米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点![]() (与
(与![]() 不重合),沿
不重合),沿![]() 修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧
修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧![]() 修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。
修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。

(1)设![]() (弧度),将绿化带的总长度表示为
(弧度),将绿化带的总长度表示为![]() 的函数
的函数![]() ;
;
(2)求绿化带的总长度![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由四个不同的数字![]() 1,2,4,
1,2,4,![]() 组成无重复数字的三位数.(最后的结果用数字表达)
组成无重复数字的三位数.(最后的结果用数字表达)
(Ⅰ)若![]() ,其中能被5整除的共有多少个?
,其中能被5整除的共有多少个?
(Ⅱ)若![]() ,其中能被3整除的共有多少个?
,其中能被3整除的共有多少个?
(Ⅲ)若![]() ,其中的偶数共有多少个?
,其中的偶数共有多少个?
(Ⅳ)若所有这些三位数的各位数字之和是252,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月10日,我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖,以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法,目前,国内青蒿人工种植发展迅速,调查表明,人工种植的青蒿的长势与海拨高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为![]() ,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标
,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标![]() 的值评定人工种植的青蒿的长势等级,若
的值评定人工种植的青蒿的长势等级,若![]() ,则长势为一级;若
,则长势为一级;若![]() ,则长势为二极;若
,则长势为二极;若![]() ,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:
,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:
种植地编号 |
|
|
|
|
|
|
|
|
|
|
|
种植地编号 |
|
|
|
|
|
|
|
|
|
|
|
(1)若该地有青蒿人工种植地180个,试估计该地中长势等级为三级的个数;
(2)从长势等级为一级的青蒿人工种植地中随机抽取两个,求这两个人工种植地的综合指标![]() 均为4个概率.
均为4个概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间满足的关系式为:![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
附:回归方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
![]()
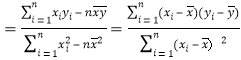 ,
,![]()
![]()
![]()
![]() .
.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为![]() 米的水轮如图所示,水轮圆心
米的水轮如图所示,水轮圆心![]() 距离水面
距离水面![]() 米;已知水轮按逆时针做匀速转动,每
米;已知水轮按逆时针做匀速转动,每![]() 秒转一圈,如果当水轮上点
秒转一圈,如果当水轮上点![]() 从水中浮现时(图中点
从水中浮现时(图中点![]() )开始计算时间.
)开始计算时间.

(1)以水轮所在平面与水面的交线为![]() 轴,以过点
轴,以过点![]() 且与水面垂直的直线为
且与水面垂直的直线为![]() 轴,建立如图所示的直角坐标系,试将点
轴,建立如图所示的直角坐标系,试将点![]() 距离水面的高度
距离水面的高度![]() (单位:米)表示为时间
(单位:米)表示为时间![]() (单位:秒)的函数;
(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点![]() 距水面的高度超过
距水面的高度超过![]() 米?
米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为![]() .若将函数y=f(x)的图象向右平移
.若将函数y=f(x)的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,则g(x)在下列区间上是减函数的是( )
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,则g(x)在下列区间上是减函数的是( )
A. ![]() B. [0,π]
B. [0,π]
C. [2π,3π] D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所发现,一种作物的年收获量![]() (单位:
(单位:![]() )与它“相近”作物的株数
)与它“相近”作物的株数![]() 具有相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有相关关系(所谓两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为![]() 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下:
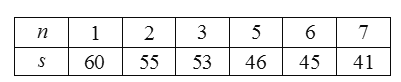
(1)根据研究发现,该作物的年收获量![]() 可能和它“相近”作物的株数
可能和它“相近”作物的株数![]() 有以下两种回归方程:
有以下两种回归方程:![]() ,利用统计知识,结合相关系数
,利用统计知识,结合相关系数![]() 比较使用哪种回归方程更合适;
比较使用哪种回归方程更合适;
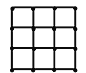
(2)农科所在如下图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每个小正方形的面积为![]() ,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
参考公式:线性回归方程为![]() ,其中
,其中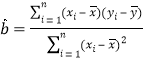 ,
,![]() ,
,
相关系数 ;
;
参考数值:![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com