已知A={x|x2+3x+2≥0},B={x|mx2-4x+m-1>0,m∈R},若A∩B=φ,且A∪B=A,求m的取值范围.
解:由已知A={x|x
2+3x+2≥0}得A={x|x≤-2}或x≥-1由A∩B=φ得.
(1)∵A非空,∴B=φ;
(2)∵A={x|x≤-2或x≥-1}∴B={x|-2<x<-1}.
另一方面,A∪B=AB⊆A,于是上面(2)不成立,
否则A∪B=R,与题设A∪B=A矛盾.
由上面分析知,B=φ.由已知B={x|mx
2-4x+m-1>0},m∈R结合B=φ,
得对一切x∈R,mx
2-4x+m-1≤0恒成立,
于是,有
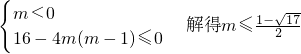
∴m的取值范围是
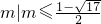
.
分析:先化简集合A={x|x
2+3x+2≥0}为A={x|x≤-2或x≥-1},再由A∩B=φ得出集合B=φ或B={x|-2<x<-1}.再由A∪B=A,得B⊆A,从而有对一切x∈R,mx
2-4x+m-1≤0恒成立,再由判别式求解.
点评:本题主要考查集合的关系及运算和用判别式法解决不等式恒成立问题.

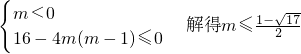
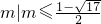 .
.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案