
【题目】已知函数![]() (
(![]() )
)
(1)若![]() 是
是![]() 的极值,求
的极值,求![]() 的值,并求
的值,并求![]() 的单调区间。
的单调区间。
(2)若![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
【答案】(1)![]() ,
,![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .(2)
.(2)![]()
【解析】
(1)计算![]() 的导函数,结合极值,计算a,结合导函数与原函数单调关系,计算单调区间,即可。(2)法一:计算导函数,构造函数
的导函数,结合极值,计算a,结合导函数与原函数单调关系,计算单调区间,即可。(2)法一:计算导函数,构造函数![]() ,结合导函数,得到
,结合导函数,得到![]() 的单调区间,计算范围,即可。法二 :构造函数
的单调区间,计算范围,即可。法二 :构造函数![]() ,结合导函数,得到原函数单调性,计算
,结合导函数,得到原函数单调性,计算![]() ,得到a的范围,即可。
,得到a的范围,即可。
(1)![]() 的定义域是
的定义域是![]() ,
,![]() ,
,
由![]() 是
是![]() 的极值得
的极值得![]() ,得
,得![]() .
.
![]() 时,由
时,由![]() ,得
,得![]() ,
,
列表(列表的功能有两个:一是检验![]() 的正确性;二是求单调区间)得
的正确性;二是求单调区间)得
|
|
|
|
| 负 | 0 | 正 |
| 单调递减 | 极小值 | 单调递增 |
综上,![]() ,
,![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
(2)法一:因![]() ,
,![]() .
.
记![]() ,
,
则![]() ,且
,且![]() ,当
,当![]() ,
,
即![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
故![]() 时,
时,![]() ,则
,则![]() ,
,
则![]() 在
在![]() 单调递增,
单调递增,![]() ,符合。
,符合。
当![]() ,即
,即![]() 时,则存在
时,则存在![]() ,使得
,使得![]() 时,
时,![]() ,
,
此时,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,![]() 时,
时,![]() ,不符。
,不符。
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
法二:![]() 时,
时,![]() ,
,![]() 等价于
等价于![]() ,
,
记![]() ,
,
则 ,
,
记![]() ,
,
则![]() ,
,
故![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
由洛必达法则得![]() ,
,
故![]() ,综上,实数
,综上,实数![]() 的取值范围是
的取值范围是![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】某年级组织学生参加了某项学术能力测试,为了解参加测试学生的成绩情况,从中随机抽取20名学生的测试成绩作为样本,规定成绩大于或等于80分的为优秀,否则为不优秀.统计结果如图:
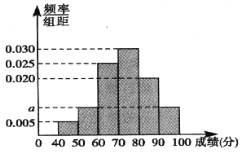
(1)求![]() 的值和样本的平均数;
的值和样本的平均数;
(2)从该样本成绩优秀的学生中任选两名,求这两名学生的成绩至少有一个落在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.

现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生周考数学成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.

(1)求图中![]() 的矩形高的值,并估计这50人周考数学的平均成绩;
的矩形高的值,并估计这50人周考数学的平均成绩;
(2)根据直方图求出这50人成绩的众数和中位数(精确到0.1);
(3)从成绩不低于80分的学生中随机选取2人,该2人中成绩不低于90分的人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两名老师和五名学生站一排拍照.
(1)五名学生必须排在一起共有多少种排法?
(2)两名老师不能相邻共有多少种排法?
(3)两名老师不能排在两边共有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.曲线
轴正半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程,曲线
的普通方程,曲线![]() 的参数方程;
的参数方程;
(2)若![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,求
上的动点,求![]() 的最小值,并求
的最小值,并求![]() 取得最小值时,
取得最小值时,![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
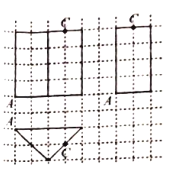
【题目】如图是放置在桌面的某三棱柱的三视图,其中网格小正方形边长为1.若三棱柱表面上的![]() 、
、![]() 两点在三视图中的对应点为
两点在三视图中的对应点为![]() 、
、![]() ,现一只蚂蚁要沿该三棱柱的表面(不包括下底面)从
,现一只蚂蚁要沿该三棱柱的表面(不包括下底面)从![]() 爬到
爬到![]() ,则所有路径里最短路径的长度为( )
,则所有路径里最短路径的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com