
【题目】西北某省会城市计划新修一座城市运动公园,设计平面如图所示:其为五边形![]() ,其中三角形区域
,其中三角形区域![]() 为球类活动场所;四边形
为球类活动场所;四边形![]() 为文艺活动场所,
为文艺活动场所,![]() ,为运动小道(不考虑宽度)
,为运动小道(不考虑宽度)![]() ,
,![]() ,
,![]() 千米.
千米.
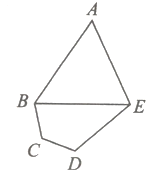
(1)求小道![]() 的长度;
的长度;
(2)求球类活动场所![]() 的面积最大值.
的面积最大值.
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】某海滨浴场一天的海浪高度![]() 是时间
是时间![]() 的函数,记作
的函数,记作![]() ,下表是某天各时的浪高数据:
,下表是某天各时的浪高数据:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)选用一个三角函数来近似描述这个海滨浴场的海浪高度![]() 与时间
与时间![]() 的函数关系;
的函数关系;
(2)依据规定,当海浪高度不少于![]() 时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的
时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的![]() 至
至![]() 之间,有多少时间可供冲浪爱好者进行冲浪?
之间,有多少时间可供冲浪爱好者进行冲浪?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 与
与![]() ,
,![]() 交于不同四点,这四点在
交于不同四点,这四点在![]() 上的排列顺次为
上的排列顺次为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,点F为抛物线C1:![]() 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2:![]() 相切于点Q.
相切于点Q.

(Ⅰ)当直线PQ的方程为![]() 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数P变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]()
(1)求证:数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,对任意
,对任意![]() ,不等式
,不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在请说明理由.
的取值范围,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有三个乡镇,分别位于一个矩形![]() 的两个顶点M,N及
的两个顶点M,N及![]() 的中点S处,
的中点S处,![]() ,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为
,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为![]() .
.
(1)设![]() ,试将L表示为x的函数并写出其定义域;
,试将L表示为x的函数并写出其定义域;
(2)试利用(1)的函数关系式确定宣讲站O的位置,使宣讲站O到三个乡镇的距离之和![]() 最小.
最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的离心率为2,过点
的离心率为2,过点![]() 、斜率为1的直线
、斜率为1的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点且
两点且![]() ,
,![]() .
.
(1)求双曲线方程。
(2)设![]() 为双曲线
为双曲线![]() 右支上动点,
右支上动点,![]() 为双曲线
为双曲线![]() 的右焦点,在
的右焦点,在![]() 轴负半轴上是否存在定点
轴负半轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com