
【题目】如图所示的平面图形中,ABCD是边长为2的正方形,△HDA和△GDC都是以D为直角顶点的等腰直角三角形,点E是线段GC的中点.现将△HDA和△GDC分别沿着DA,DC翻折,直到点H和G重合为点P.连接PB,得如图的四棱锥.
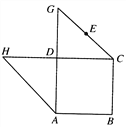
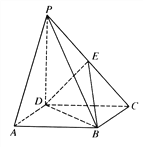
(Ⅰ)求证:PA//平面EBD;
(Ⅱ)求二面角![]() 大小.
大小.
【答案】(Ⅰ)见解析;(Ⅱ)60o.
【解析】试题分析:(1)连接AC交BD于点O,连接EO,由EO为△CPA的中位线,能证明PA//平面EDB (2)分别求出平面PBD和PBC的法向量,利用向量法能求出二面角的大小
试题解析:
(Ⅰ)证明:连接AC交BD于点O,
连接EO,因为四边形ABCD
是正方形,所以O为AC的中点,
又因为E为PC中点,
所以EO为△CPA的中位线,
所以EO//PA
因为EO![]() 平面EDB,PA
平面EDB,PA![]() 平面EDB
平面EDB
所以PA//平面EDB
(Ⅱ)由题意有![]() ,
,
故DA,DC,DP两两垂直
如图,以D为原点建立空间直角坐标系![]()
有![]()
由题知![]()
又因为AC![]() 平面ABCD,所以
平面ABCD,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]()
所以平面PBD的法向量是![]()
设平面PBC的法向量![]() ,
,
由于![]() ,
,![]()
则有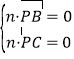 ,所以
,所以![]()
令![]() ,得
,得![]()
则![]()
由图可知求二面角![]() 的平面角为锐角,
的平面角为锐角,
所以二面角![]() 的大小为60o
的大小为60o


科目:高中数学 来源: 题型:
【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸离出发地的路程为1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
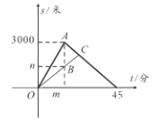
(1)图中![]() ________,
________, ![]() _______;
_______;
(2)求小明和爸爸相遇的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1中,E,F分别是AB,AA1的中点.
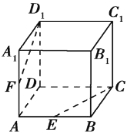
求证:(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于命题![]() :存在一个常数
:存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() 恒成立.
恒成立.
(1)试给出这个常数![]() 的值;
的值;
(2)在(1)所得结论的条件下证明命题![]() ;
;
(3)对于上述命题,某同学正确地猜想了命题![]() :“存在一个常数
:“存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() ,
,![]() 恒成立.”观察命题
恒成立.”观察命题![]() 与命题
与命题![]() 的规律,请猜想与正数
的规律,请猜想与正数![]() ,
,![]() ,
,![]() ,
,![]() 相关的命题.
相关的命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布
N(-1,1)的部分密度曲线)的点的个数的估计值为
附:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.682 6,P(μ-2σ<X<μ+2σ)=0.954 4.
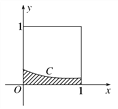
A. 1 193 B. 1 359 C. 2 718 D. 3 413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据悉遵义市红花岗区、汇川区2017年现有人口总数为110万人,如果年自然增长率为![]() %,试解答以下问题:
%,试解答以下问题:
(1)写出经过![]() 年后,遵义市人口总数
年后,遵义市人口总数![]() (单位:万人)关于
(单位:万人)关于![]() 的函数关系式;
的函数关系式;
(2)计算10年以后遵义市人口总数(精确到0.1万人);
(3)计算经过多少年后遵义市人口将达到150万人(精确到1年)
(参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们可以用随机模拟的方法估计![]() 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数![]() 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生![]() 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为![]() ,则由此可估计
,则由此可估计![]() 的近似值为( )
的近似值为( )
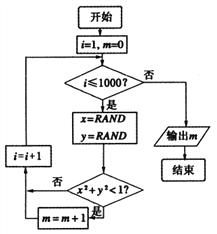
A. 3.119 B. 3.124 C. 3.132 D. 3.151
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有红、白两种颜色的小球共7个,它们除颜色外完全相同,从中任取2个,都是白色小球的概率为![]() ,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
(1)求![]() ;
;
(2)求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,圆
,圆![]() ,点
,点![]() 为抛物线
为抛物线![]() 上的动点,
上的动点,![]() 为坐标原点,线段
为坐标原点,线段![]() 的中点
的中点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 上的点,过点
上的点,过点![]() 作圆
作圆![]() 的两条切线,分别与
的两条切线,分别与![]() 轴交于
轴交于![]() 两点.
两点.
求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com