科目：高中数学 来源：南通高考密卷·数学（理） 题型：044
已知向量p＝(a，x＋1)，q＝(x，a)，m＝(1，y)，且(p－q)∥m，y与x的函数关系式为y＝f(x)．
(1)求f(x)；
(2)判断并证明函数y＝f(x)当x＞a时的单调性；
(3)我们利用函数y＝f(x)构造一个数列{xn)，方法如下：对于f(x)定义域中的x1，令x2＝f(x1)，x3＝f(x2)，…，xn＝f(xn－1)，…．在上述构造数列的过程中，如果xi(i＝1，2，3，4，…)在定义域中，构造数列的过程将继续下去；如果xi不在定义域中，则构造数列的过程停止．如果取f(x)定义域中任一值作为x1，都可以用上述方法构造出一个无穷数列{xn}，求实数a的值．
查看答案和解析>>
科目：高中数学 来源：训练必修三数学人教A版 人教A版 题型：013
已知a＝3，b＝5，c＝4，经过下面这个程序运行之后其结果是
INPUT “a，b，c＝”；3，5，4
IF b＞a THEN
t＝a
a＝b
b＝t
END IF
IF c＞a THEN
t＝a
a＝c
c＝t
END IF
IF c＞b THEN
t＝b
b＝c
c＝t
END IF
PRINT a，b，c
END
a＝3，b＝5，c＝4
a＝5，b＝4，c＝3
a＝5，b＝3，c＝4
a＝3，b＝4，c＝5
查看答案和解析>>
科目：高中数学 来源：四川省成都市2011届高三第一次诊断性检测数学文科试题 题型：022
已知非零向量
、
、
、
满足：
＋β＋γ(α，β，γ∈R)，B、C、D为不共线三点，给出下列命题：
①若α
＝
，β＝
，γ＝－1，则A、B、C、D四点在同一平面上；
②若α
＝β＝γ＝?，?|＋||＋||＝1，＜，＞＝＜，＞＝
，＜，＞＝
，则||＝2；
③已知正项等差数列
{an}(n∈N*)，若α＝a2，β＝a2009，γ＝0，且A、B、C三点共线，但O点不在直线BC上，则
＋
的最小值为10；
④若α
＝
，β＝－
，γ＝0，则A、B、C三点共线且A分
所成的比λ一定为－4
其中你认为正确的所有命题的序号是
________查看答案和解析>>
科目：高中数学 来源：2010-2011学年本溪县高三暑期补课阶段考试数学卷 题型：解答题
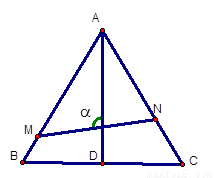
（本题12分）如图，已知△ABC是边长为1的正三角形，M、N分别是
边AB、AC上的点，线段MN经过△ABC的中心G，设ÐMGA＝a（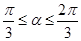
）
（1）试将△AGM、△AGN的面积（分别记为S1与S2）表示为a的函数
（2）求y＝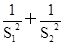
的最大值与最小值
查看答案和解析>>
科目：高中数学 来源：2014届山东省高一第二学期期中考试数学试卷（解析版） 题型：解答题
已知sina＝
,aÎ(
,p)，cosb＝－
，b是第三象限的角.
⑴ 求cos(a－b)的值；
⑵ 求sin(a＋b)的值；
⑶ 求tan2a的值.
【解析】第一问中∵ aÎ(,p),∴ cosa＝－
＝－
, ∵ b是第三象限的角，
∴ sinb＝－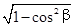
＝－
,
cos(a－b)＝cosa·cosb＋sina·sinb ＝(－)×(－)＋×(－)＝－
⑵ 中sin(a＋b)＝sina·cosb＋cosa·sinb ＝×(－)＋(－)×(－)＝
⑶ 利用二倍角的正切公式得到。∵tana＝
＝－
∴tan2a＝
＝
＝－
解∵ aÎ(,p),∴ cosa＝－＝－, …………1分
∵ b是第三象限的角，∴ sinb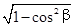＝－＝－, ………2分
⑴ cos(a－b)＝cosa·cosb＋sina·sinb …………3分
＝(－)×(－)＋×(－)＝－
………………5分
⑵ sin(a＋b)＝sina·cosb＋cosa·sinb ……………………6分
＝×(－)＋(－)×(－)＝
…………………8分
⑶ ∵tana＝＝－
…………………9分
∴tan2a＝
………………10分
＝＝－
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
|＝
,|
|＝
,
，则
