
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() ,且函数
,且函数![]() =
= ![]() 是偶函数
是偶函数
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,求函数
,求函数![]() 在
在![]() 的最大值和最小值
的最大值和最小值
(3)函数![]() 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
【答案】(1) ![]() =
=![]() .(2)答案见解析;(3)函数
.(2)答案见解析;(3)函数![]() 的图象上存在符合要求的点的坐标为
的图象上存在符合要求的点的坐标为![]()
【解析】试题分析:(1)因为函数![]() 是偶函数,所以二次函数
是偶函数,所以二次函数![]() 的对称轴方程为
的对称轴方程为![]() ,由此求得
,由此求得![]() 的值;(2)由(1)可得
的值;(2)由(1)可得![]() ,讨论
,讨论![]() 的范围,进而求出
的范围,进而求出![]() 的最值;(3)如果函数
的最值;(3)如果函数![]() 的图象上存在符合要求的点,设为
的图象上存在符合要求的点,设为![]() ,从而
,从而![]() ,由此求得
,由此求得![]() 、
、![]() 的值,从而得出结论.
的值,从而得出结论.
试题解析:(1)因为函数![]() 是偶函数,
是偶函数,
所以二次函数![]() 的对称轴方程为
的对称轴方程为![]() ,即
,即![]()
所以![]()
又因为二次函数![]() 的图象经过点
的图象经过点![]()
所以![]() ,解得
,解得![]() .
.
因此,函数![]() 的解析式为
的解析式为![]() =
=![]() .
.
(2)由(1)知, ![]() =
=![]() =
=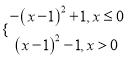 ,
,
所以,当![]() 时,
时, ![]() =
=![]() .
.
当![]() =
=![]()
当![]()
当![]() =
= ![]() =
=![]() .
.
(3)如果函数![]() 的图象上存在点
的图象上存在点![]() 符合要求其中
符合要求其中![]()
则![]() ,从而
,从而![]() =
=![]() ,
,
即![]() =
=![]() .
.
注意到43是质数,且![]()
所以有 ,
,
解得![]() ,
,
因此,函数![]() 的图象上存在符合要求的点的坐标为
的图象上存在符合要求的点的坐标为![]()


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
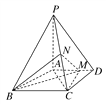
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
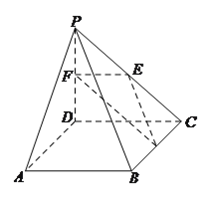
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )在线段
)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy 中,已知圆C的参数方程为 ![]() (φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)求圆的极坐标方程;
(2)直线l的极坐方程是 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表,若成绩120分以上(含120分)为优秀.
分数区间 | 甲班频率 | 乙班频率 |
[0,30) | 0.1 | 0.2 |
[30,60) | 0.2 | 0.2 |
[60,90) | 0.3 | 0.3 |
[90,120) | 0.2 | 0.2 |
[120,150] | 0.2 | 0.1 |
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
(Ⅰ)求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成上面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元.某月甲、乙两户共交水费y元,已知甲、乙两用户该月用水量分别为5x,3x吨. (Ⅰ) 若x=1,求该月甲、乙两户的水费;
(Ⅱ) 求y关于x的函数;
(Ⅲ) 若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧棱A1A⊥底面ABC,AC=1,AA1=2,∠BAC=90°,若直线AB1与直线A1C的夹角的余弦值是 ![]() ,则棱AB的长度是 .
,则棱AB的长度是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com