练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中,曲线C1的参数方程为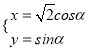 (α为参数),以原点O为极点,x轴的正半轴为级轴,建立极坐标系,曲线C2的极坐标方程;

    (1)求曲线C1的普通方程和曲线C2的直角坐标方程;

    (2)设P为曲线C1上的动点,求点P到曲线C2上的距离的最小值.

    【答案】（1）C1的普通方程为: 曲线C2：x+y=6；（2）.

    【解析】试题分析：(1)消去参数α可得曲线C1的普通方程;利用化简可得曲线C2的直角坐标方程;

    (2)设椭圆上的点,利用点到直线的距离公式,结合三角函数的知识求解即可.

    试题解析：

    (1)由曲线C1: 为参数),

    曲线C1的普通方程为:

    由曲线C2:ρsin(π+)=3,展开可得:

    (sinθ+cosθ)=3,

    化为:x+y=6.

    (2)椭圆上的点到直线O的距离为

    其中,

    所以当sin(α+φ)=1时,P的最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】（本题满分14分）如图，已知椭圆：，其左右焦点为及，过点的直线交椭圆于两点，线段的中点为，的中垂线与轴和轴分别交于两点，且、、构成等差数列.

    （1）求椭圆的方程；

    （2）记△的面积为，△（为原点）的面积为．试问：是否存在直线，使得？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一盒中装有除颜色外其余均相同的12个小球，从中随机取出1个球，取出红球的概率为，取出黑球的概率为，取出白球的概率为，取出绿球的概率为.求：

    (1)取出的1个球是红球或黑球的概率；

    (2)取出的1个球是红球或黑球或白球的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知四棱锥中， 平面，底面是菱形，且． ， 、的中点分别为， ．

    （Ⅰ）求证．

    （Ⅱ）求二面角的余弦值．

    （Ⅲ）在线段上是否存在一点，使得平行于平面？若存在，指出在上的位置并给予证明，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）求不等式;

    （Ⅱ）若函数的最小值为，且，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知定圆，定直线，过的一条动直线与直线相交于，与圆相交于，两点，是中点.

    （Ⅰ）当与垂直时，求证：过圆心；

    （Ⅱ）当时，求直线的方程；

    （Ⅲ）设，试问是否为定值，若为定值，请求出的值；若不为定值，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

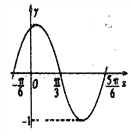
    【题目】如图是函数在区间上的图象，为了得到这个函数的图象，只需将y=sinx的图象

    A. 向左平移个长度单位，再把所得各点的横坐标变为原来的，纵坐标不变

    B. 向左平移至个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变

    C. 向左平移个长度单位，再把所得各点的横坐标变为原来的，纵坐标不变

    D. 向左平移个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】读下列各题所给的程序，依据程序画出程序框图，并说明其功能：

    (1)INPUT “x＝”；x

    IF x>1 OR x<－1 THEN

    y＝1

    ELSE y＝0

    END IF

    PRINE y

    END

    (2)INPUT “输入三个正数a，b，c＝”；a，b，c

    IF a＋b>c AND a＋c>b AND b＋c>a THEN

    p＝(a＋b＋c)/2

    S＝SQR(p*(p－a)*(p－b)*(p－c))

    PRINT “三角形的面积S＝”S

    ELSE

    PRINT “构不成三角形”

    END IF

    END

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中， ．

    （Ⅰ）当时， 的零点为______；（将结果直接填写在横线上）

    （Ⅱ）当时，如果存在，使得，试求的取值范围；

    （Ⅲ）如果对于任意，都有成立，试求的最大值．

    查看答案和解析>>

    同步练习册答案