
ЁОЬтФПЁПИљОнвдЭљЕФОбщЃЌФГЙЄГЬЪЉЙЄЦкМфЕФНЋЪ§СПXЃЈЕЅЮЛЃКmmЃЉЖдЙЄЦкЕФгАЯьШчЯТБэЃК
НЕЫЎСПX | XЃМ300 | 300ЁмXЃМ700 | 700ЁмXЃМ900 | XЁн900 |
ЙЄЦкбгЮѓЬьЪ§Y | 0 | 2 | 6 | 10 |
РњФъЦјЯѓзЪСЯБэУїЃЌИУЙЄГЬЪЉЙЄЦкМфНЕЫЎСПXаЁгк300ЃЌ700ЃЌ900ЕФИХТЪЗжБ№ЮЊ0.3ЃЌ0.7ЃЌ0.9ЃЌЧѓЃК
ЃЈ1ЃЉЙЄЦкбгЮѓЬьЪ§YЕФОљжЕгыЗНВюЃЛ
ЃЈ2ЃЉдкНЕЫЎСПXжСЩйЪЧ300ЕФЬѕМўЯТЃЌЙЄЦкбгЮѓВЛГЌЙ§6ЬьЕФИХТЪЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКгЩЬтвтЃЌ
PЃЈXЃМ300ЃЉ=0.3ЃЌPЃЈ300ЁмXЃМ700ЃЉ=PЃЈXЃМ700ЃЉЉPЃЈXЃМ300ЃЉ=0.7Љ0.3=0.4ЃЌPЃЈ700ЁмXЃМ900ЃЉ=PЃЈXЃМ900ЃЉЉPЃЈXЃМ700ЃЉ=0.9Љ0.7=0.2ЃЌPЃЈXЁн900ЃЉ=1Љ0.9=0.1
YЕФЗжВМСаЮЊ
Y | 0 | 2 | 6 | 10 |
P | 0.3 | 0.4 | 0.2 | 0.1 |
ЁрEЃЈYЃЉ=0ЁС0.3+2ЁС0.4+6ЁС0.2+10ЁС0.1=3
DЃЈYЃЉ=ЃЈ0Љ3ЃЉ2ЁС0.3+ЃЈ2Љ3ЃЉ2ЁС0.4+ЃЈ6Љ3ЃЉ2ЁС0.2+ЃЈ10Љ3ЃЉ2ЁС0.1=9.8
ЁрЙЄЦкбгЮѓЬьЪ§YЕФОљжЕЮЊ3ЃЌЗНВюЮЊ9.8ЃЛ
ЃЈ2ЃЉ
НтЃКPЃЈXЁн300ЃЉ=1ЉPЃЈXЃМ300ЃЉ=0.7ЃЌPЃЈ300ЁмXЃМ900ЃЉ=PЃЈXЃМ900ЃЉЉPЃЈXЃМ300ЃЉ=0.9Љ0.3=0.6
гЩЬѕМўИХТЪПЩЕУPЃЈYЁм6|XЁн300ЃЉ= ![]()
ЁОНтЮіЁПЃЈ1ЃЉгЩЬтвтЃЌИУЙЄГЬЪЉЙЄЦкМфНЕЫЎСПXаЁгк300ЃЌ700ЃЌ900ЕФИХТЪЗжБ№ЮЊ0.3ЃЌ0.7ЃЌ0.9ЃЌНсКЯФГГЬЪЉЙЄЦкМфЕФНЕЫЎСПЖдЙЄЦкЕФгАЯьЃЌПЩЧѓЯргІЕФИХТЪЃЌНјЖјПЩЕУЦкбгЮѓЬьЪ§YЕФОљжЕгыЗНВюЃЛЃЈ2ЃЉРћгУИХТЪЕФМгЗЈЙЋЪНПЩЕУPЃЈXЁн300ЃЉ=1ЉPЃЈXЃМ300ЃЉ=0.7ЃЌPЃЈ300ЁмXЃМ900ЃЉ=PЃЈXЃМ900ЃЉЉPЃЈXЃМ300ЃЉ=0.9Љ0.3=0.6ЃЌРћгУЬѕМўИХТЪЃЌМДПЩЕУЕННсТл



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж14ЗжЃЉШчЭМ,дкЫФРтзЖ![]() жаЃЌ
жаЃЌ ![]() ЦНУц
ЦНУц![]() ЃЌЕзУц
ЃЌЕзУц![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ ![]() ЃЌ
ЃЌ ![]() ЮЊ
ЮЊ![]() гы
гы![]() ЕФНЛЕуЃЌ
ЕФНЛЕуЃЌ ![]() ЮЊ
ЮЊ![]() ЩЯШЮвтвЛЕуЃЎ
ЩЯШЮвтвЛЕуЃЎ

ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЦНУц
ЦНУц![]() ЃЌВЂЧвЖўУцНЧ
ЃЌВЂЧвЖўУцНЧ![]() ЕФДѓаЁЮЊ
ЕФДѓаЁЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЕФИїЯюОљЮЊе§Ъ§ЃЌЧА
ЕФИїЯюОљЮЊе§Ъ§ЃЌЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЧв
ЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓжЄЃКЪ§Са![]() ЪЧЕШВюЪ§СаЃЛ
ЪЧЕШВюЪ§СаЃЛ
ЃЈ2ЃЉШєЪ§Са![]() Тњзу
Тњзу![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхдкЃЈЉЁоЃЌ0ЃЉЁШЃЈ0ЃЌ+ЁоЃЉЩЯЕФКЏЪ§fЃЈxЃЉЃЌзмгаfЃЈmnЃЉ=fЃЈmЃЉfЃЈnЃЉЃЌЧвfЃЈxЃЉЃО0ЃЌЕБxЃО1ЪБЃЌfЃЈxЃЉЃО1ЃЎ
ЃЈ1ЃЉЧѓfЃЈ1ЃЉЃЌfЃЈЉ1ЃЉЕФжЕЃЛ
ЃЈ2ЃЉХаЖЯКЏЪ§ЕФЦцХМадЃЌВЂжЄУїЃЛ
ЃЈ3ЃЉХаЖЯКЏЪ§дкЃЈ0ЃЌ+ЁоЃЉЩЯЕФЕЅЕїадЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЪ§Са![]() ЃК
ЃК ![]() ЃЌ
ЃЌ ![]() ЃЌЁЃЌ
ЃЌЁЃЌ ![]() ЃЈ
ЃЈ![]() ЃЉжа
ЃЉжа![]() ЃЈ
ЃЈ![]() ЃЉЧвЖдШЮвтЕФ
ЃЉЧвЖдШЮвтЕФ![]()
![]() КуГЩСЂЃЌдђГЦЪ§Са
КуГЩСЂЃЌдђГЦЪ§Са![]() ЮЊЁА
ЮЊЁА![]() Ъ§СаЁБЃЎ
Ъ§СаЁБЃЎ
ЃЈЂёЃЉШєЪ§Са![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЮЊЁА
ЮЊЁА![]() Ъ§СаЁБЃЌаДГіЫљгаПЩФмЕФ
Ъ§СаЁБЃЌаДГіЫљгаПЩФмЕФ![]() ЃЌ
ЃЌ ![]() ЃЛ
ЃЛ
ЃЈЂђЃЉШєЁА![]() Ъ§СаЁБ
Ъ§СаЁБ![]() ЃК
ЃК ![]() ЃЌ
ЃЌ ![]() ЃЌЁЃЌ
ЃЌЁЃЌ ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈЂѓЃЉЩш![]() ЮЊИјЖЈЕФХМЪ§ЃЌЖдЫљгаПЩФмЕФЁА
ЮЊИјЖЈЕФХМЪ§ЃЌЖдЫљгаПЩФмЕФЁА![]() Ъ§СаЁБ
Ъ§СаЁБ![]() ЃК
ЃК ![]() ЃЌ
ЃЌ ![]() ЃЌЁЃЌ
ЃЌЁЃЌ ![]() ЃЌ
ЃЌ
МЧ![]() ЃЌЦфжа
ЃЌЦфжа![]() БэЪО
БэЪО![]() ЃЌ
ЃЌ ![]() ЃЌЁЃЌ
ЃЌЁЃЌ ![]() ет
ет![]() ИіЪ§жазюДѓЕФЪ§ЃЌЧѓ
ИіЪ§жазюДѓЕФЪ§ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ= ![]() sinxcosx+sin2xЉ
sinxcosx+sin2xЉ ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓfЃЈxЃЉЕФзюаЁе§жмЦкМАЦфЖдГЦжсЗНГЬЃЛ
ЃЈ2ЃЉЩшКЏЪ§gЃЈxЃЉ=fЃЈ ![]() +
+ ![]() ЃЉЃЌЦфжаГЃЪ§ІиЃО0ЃЌ|Іе|ЃМ
ЃЉЃЌЦфжаГЃЪ§ІиЃО0ЃЌ|Іе|ЃМ ![]() ЃЎ ЃЈiЃЉЕБІи=4ЃЌІе=
ЃЎ ЃЈiЃЉЕБІи=4ЃЌІе= ![]() ЪБЃЌКЏЪ§y=gЃЈxЃЉЉ4ІЫfЃЈxЃЉдк[
ЪБЃЌКЏЪ§y=gЃЈxЃЉЉ4ІЫfЃЈxЃЉдк[ ![]() ЃЌ
ЃЌ ![]() ]ЩЯЕФзюДѓжЕЮЊ
]ЩЯЕФзюДѓжЕЮЊ ![]() ЃЌЧѓІЫЕФжЕЃЛ
ЃЌЧѓІЫЕФжЕЃЛ
ЃЈiiЃЉШєКЏЪ§gЃЈxЃЉЕФвЛИіЕЅЕїМѕЧјМфФкгавЛИіСуЕуЉ ![]() ЃЌЧвЦфЭМЯѓЙ§ЕуAЃЈ
ЃЌЧвЦфЭМЯѓЙ§ЕуAЃЈ ![]() ЃЌ1ЃЉЃЌМЧКЏЪ§gЃЈxЃЉЕФзюаЁе§жмЦкЮЊTЃЌЪдЧѓTШЁзюДѓжЕЪБКЏЪ§gЃЈxЃЉЕФНтЮіЪНЃЎ
ЃЌ1ЃЉЃЌМЧКЏЪ§gЃЈxЃЉЕФзюаЁе§жмЦкЮЊTЃЌЪдЧѓTШЁзюДѓжЕЪБКЏЪ§gЃЈxЃЉЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЙХЯЃРАБЯДяИчРЫЙбЇХЩАб1ЃЌ3ЃЌ6ЃЌ10ЃЌ15ЃЌ21ЃЌ28ЃЌЁетаЉЪ§НазіШ§НЧаЮЪ§ЃЌвђЮЊетаЉЪ§ЖдгІЕФЕуПЩвдХХГЩвЛИіе§Ш§НЧаЮдђЕкnИіШ§НЧаЮЪ§ЮЊ ЃЎ 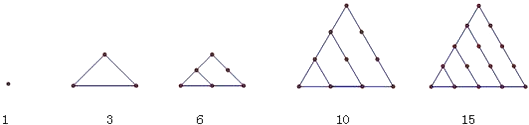
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкМИКЮЬхжаЃЌЫФБпаЮ![]() ЮЊСтаЮЃЌЖдНЧЯп
ЮЊСтаЮЃЌЖдНЧЯп![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЮЊЬнаЮЃЌ
ЮЊЬнаЮЃЌ ![]() .
.

ЃЈЂёЃЉШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂѓЃЉШє![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЧѓ
ЃЌЧѓ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧ.
ЫљГЩНЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцЛњГщШЁФГжабЇИпШ§ФъМЖМзввСНАрИї10УћЭЌбЇЃЌВтСПГіЫћУЧЕФЩэИпЃЈЕЅЮЛЃКcmЃЉЃЌЛёЕУЩэИпЪ§ОнЕФОЅвЖЭМШчЭМЃЎЦфжаМзАргавЛИіЪ§ОнБЛЮлЫ№ЃЎ
ЃЈЂёЃЉШєвбжЊМзАрЭЌбЇЩэИпЦНОљЪ§ЮЊ170cmЃЌЧѓЮлЫ№ДІЕФЪ§ОнЃЛ
ЃЈЂђЃЉЯжДгввАрет10УћЭЌбЇжаЫцЛњГщШЁСНУћЩэИпВЛЕЭгк173cmЕФЭЌбЇЃЌЧѓЩэИпЮЊ176cmЕФЭЌбЇБЛГщжаЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com