
(本题13分)
已知函数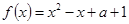
(1)若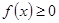 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数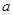 的取值范围.
的取值范围.
(2)求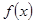 在区间
在区间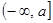 上的最小值
上的最小值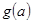 的表达式.
的表达式.
科目:高中数学 来源: 题型:解答题
(本题满分15分)
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: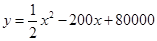 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数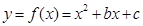 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线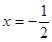 对称。
对称。
(1)求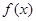 的解析式。
的解析式。
(2)已知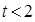 ,
,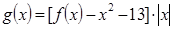 ,
,
① 若函数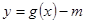 的零点有三个,求实数
的零点有三个,求实数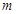 的取值范围;
的取值范围;
②求函数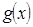 在[
在[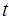 ,2]上的最小值。
,2]上的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
有甲、乙两种商品,经销这两种商品所获的利润依次为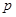 (万元)和
(万元)和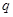 (万元),它们与投入的资金
(万元),它们与投入的资金 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: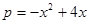 ,
, 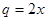 今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装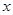 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且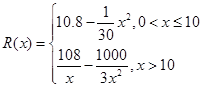 .
.
(I)写出年利润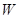 (万元)关于年产量
(万元)关于年产量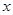 (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分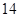 分)
分)
若函数 在定义域
在定义域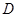 内某区间
内某区间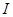 上是增函数,而
上是增函数,而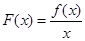 在
在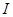 上是减函数,
上是减函数,
则称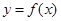 在
在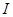 上是“弱增函数”
上是“弱增函数”
(1)请分别判断 =
=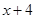 ,
,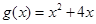 在
在 是否是“弱增函数”,
是否是“弱增函数”,
并简要说明理由;
(2)证明函数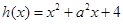 (
( 是常数且
是常数且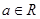 )在
)在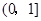 上是“弱增函数”.
上是“弱增函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)
如图,在半径为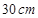 的
的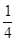 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料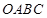 ,其中点
,其中点 在圆上,点
在圆上,点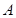 、
、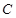 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮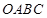 卷成一个以
卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长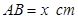 ,圆柱的体积为
,圆柱的体积为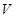
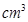 .
.
(1)写出体积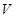 关于
关于 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积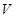 最大?最大体积是多少?
最大?最大体积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com