
已知定点F(0,1)和直线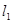 :y=-1,过定点F与直线
:y=-1,过定点F与直线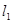 相切的动圆圆心为点C.
相切的动圆圆心为点C.
(1)求动点C的轨迹方程;
(2)过点F的直线 交动点C的轨迹于两点P、Q,交直线
交动点C的轨迹于两点P、Q,交直线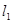 于点R,求
于点R,求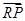 ·
· 的最小值;
的最小值;
(3)过点F且与 垂直的直线
垂直的直线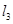 交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
科目:高中数学 来源: 题型:解答题
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).
(1)若设休闲区的长和宽的比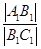 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔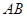 、
、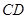 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知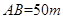 ,
,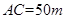 ,当
,当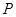 为
为 中点时,
中点时,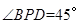 .
.
(1)求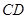 的长;
的长;
(2)试问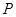 在线段
在线段 的何处时,
的何处时,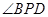 达到最大.
达到最大.
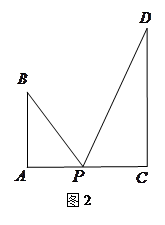
|
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
观察下列两个结论:
(Ⅰ)若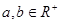 ,且
,且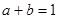 ,则
,则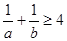 ;
;
(Ⅱ)若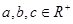 ,且
,且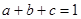 ,则
,则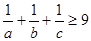 ;
;
先证明结论(Ⅱ),再类比(Ⅰ)(Ⅱ)结论,请你写出一个关于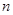 个正数
个正数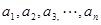 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com