设函数f(x)是定义在[-1,0)∪(0,1]上的偶函数,当x∈[-1,0)时,f(x)=x3-ax(a∈R).
(1)当x∈(0,1]时,求f(x)的解析式;
(2)若a>3,试判断f(x)在(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值1?
【答案】
分析:(1)先由函数是偶函数得f(-x)=f(x),然后将所求区间利用运算转化到已知区间上,代入到[-1,0)时,f(x)=x
3-ax即可求出在(0,1]上,函数的解析式.
(2)先求导函数,然后利用导数的符号确定函数f(x)在(0,1]上的单调性;
(3)讨论a,分别利用导数研究函数在(0,1]上的最值,然后建立等式关系,解之即可.
解答:解:(I)设x∈(0,1],则-x∈[-1,0),
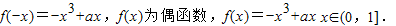
----------(3分)
(II)f'(x)=-3x
2+a,∵x∈(0,1]⇒3x
2∈[-3,0),
又a>3,∴a-3x
2>0,即f'(x)>0,∴f(x)在(0,1]上为增函数.-------------------7 分
(III)当a>3时,f(x)在(0,1]上是增函数,f
max(x)=f(1)=a-1=1⇒a=2.
(不合题意,舍去)---8 分
当
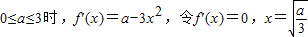
.如下表:
∴

,
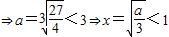
.------(10分)
当a<0时,f'(x)=a-3x
2<0,f(x)在(0,1]上单调递减,f(x)在(0,1]无最大值.
∴存在
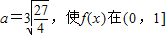
上有最大值1.--------------------------(12分)
点评:本题主要考查了解析式的求解以及函数的单调性,同时考查了利用导数研究闭区间上的最值,属于中档题.

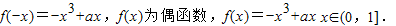 ----------(3分)
----------(3分)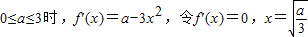 .如下表:
.如下表: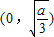
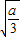
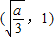
 ,
,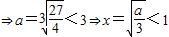 .------(10分)
.------(10分)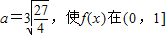 上有最大值1.--------------------------(12分)
上有最大值1.--------------------------(12分)
