
【题目】已知![]() ,函数
,函数![]() (
(![]() 是自然对数的底数)
是自然对数的底数)
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 内无零点,求
内无零点,求![]() 的最大值.
的最大值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)求出函数
的减区间;(2)求出函数![]() 求其导函数
求其导函数![]() ,可知当
,可知当![]() 时函数
时函数![]() 在区间
在区间![]() 上单调递减,可得
上单调递减,可得![]() ,函数
,函数![]() 在区间
在区间![]() 上无零点;当
上无零点;当![]() 时,分
时,分![]() 和
和![]() 分类讨论,即可筛选出函数
分类讨论,即可筛选出函数![]() 在区间
在区间![]() 内无零点的
内无零点的![]() 的范围.
的范围.
详解:(1)∵![]()
∴![]()
当![]() 时,在
时,在![]() 上
上![]() 恒成立,
恒成立,![]() 增区间为
增区间为![]() ,无减区间;
,无减区间;
当![]() 时,令
时,令![]() 得
得![]()
![]() 的增区间为
的增区间为![]() ,减区间为.
,减区间为.![]()
(2)函数![]()
![]() ,
,![]()
∴![]()
①当![]() 时,
时,![]() 在
在![]() 上恒成立,函数
上恒成立,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() ,
,
∴![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无零点;
上无零点;
②当![]() 时,令
时,令![]() 得,
得,![]()
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
因此,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(i)当![]() ,即时
,即时![]() ,
,
函数![]() 的单调递减区间是
的单调递减区间是![]() ,∴
,∴![]()
要使函数![]() 在区间
在区间![]() 内无零点,则
内无零点,则![]() ,得
,得![]() ;
;
(ii)当![]() ,即
,即![]() 时,
时,
函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,
,
∴![]()
![]()
设![]()
∴![]()
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]()
![]() ,
,
而当![]() 时,
时,![]() ,
,
∴函数![]() 在区间
在区间![]() 内有零点,不合题意.
内有零点,不合题意.
综上,要使函数![]() 在区间
在区间![]() 内无零点,则
内无零点,则![]() 的最大值为
的最大值为![]()


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() .某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
.某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
(1)求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)设![]() 表示这4名观众中认为《流浪地球》好看的人数,求
表示这4名观众中认为《流浪地球》好看的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两校分别有120名、100名学生参加了某培训机构组织的自主招生培训,考试结果出来以后,培训机构为了进一步了解各校所培训学生通过自主招生的情况,从甲校随机抽取60人,从乙校随机抽取50人进行分析,相关数据如下表.

(1)完成上面![]() 列联表,并据此判断是否有99%的把握认为自主招生通过情况与学生所在学校有关;
列联表,并据此判断是否有99%的把握认为自主招生通过情况与学生所在学校有关;
(2)现从甲、乙两校通过的学生中采取分层抽样的方法抽取5人,再从所抽取的5人种随机抽取2人,求2人全部来自于乙校的概率.
参考公式:![]() .
.
参考数据:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a≠0),设函数y=[f(x)]2+pf(x)+q的零点所组成的集合为A,则以下集合不可能是A集合的序号为__.
①![]()
②![]()
③{﹣2,3,8}
④{﹣4,﹣1,0,2}
⑤{1,3,5,7}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业产值在2008年~2017年的年增量(即当年产值比前一年产值增加的量)统计图如图所示(单位:万元),下列说法正确的是( )
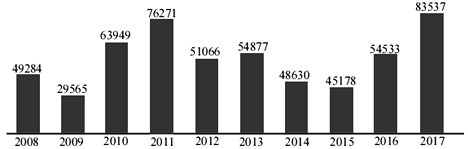
A. 2009年产值比2008年产值少
B. 从2011年到2015年,产值年增量逐年减少
C. 产值年增量的增量最大的是2017年
D. 2016年的产值年增长率可能比2012年的产值年增长率低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面 ABCD为矩形,侧面为正三角形,且平面
中,底面 ABCD为矩形,侧面为正三角形,且平面![]() 平面
平面 ![]() E 为 PD 中点,AD=2.
E 为 PD 中点,AD=2.
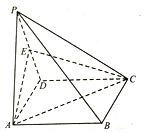
(1)证明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
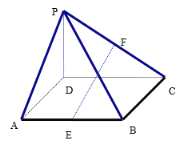
(1)求证:AB⊥平面PAD;
(2)求证:EF//平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com