练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

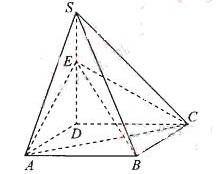
    如图，四棱锥S＝ABCD的底面是正方形，SD⊥平面ABCD,SD＝AD＝a,点E是SD上的点，且DE＝a(0<1).      

    (Ⅰ)求证：对任意的（0、1），都有AC⊥BE:

    (Ⅱ)若二面角C-AE-D的大小为600C，求的值。

    （Ⅰ）证明：连接BD，由底面是正方形可得ACBD。

       SD平面ＡＢＣＤ，BD是BE在平面ABCD上的射影，

    由三垂线定理得ACBE.

    (II) 解析：SD平面ABCD，ＣＤ平面ＡＢＣＤ， SDCD.

    又底面ＡＢＣＤ是正方形， ＣDＡD，又ＳＤAD=D，CD平面SAD。

    过点D在平面SAD内做DFAE于F，连接CF，则CFAE，

    故CFD是二面角C-AE-D 的平面角，即CFD=60°

    在Rt△ADE中，AD=, DE= ， AE= 。

    于是，DF=

    在Rt△CDF中，由cot60°=

    得，       即=3      

    ， 解得=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

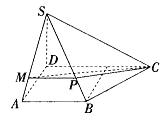
    如图，四棱锥S—ABCD中，底面ABCD是直角梯形，∠BAD＝∠ADC＝90°，AB＝AD＝a，DC＝2a，SD＝a，SD⊥平面ABCD．

    　　（1）证明：该四棱锥的四个侧面都是直角三角形；

    　　（2）设M∈SA，SM＝x，平面CDMSB＝P，证明四边形CDMP也是直角梯形，并用a与x表示；

    　　（3）x为何值时，CM最短，并求出其最短距离．

     

    查看答案和解析>>

    科目：高中数学 来源：2010年普通高等学校招生全国统一考试、文科数学(全国一) 题型：044

    如图，四棱锥S－ABCD中，SD⊥底面ABCD，AB∥DC，AD⊥DC，AB＝AD＝1，DC＝SD＝2，E为棱SB上的一点，平面EDC⊥平面SBC．

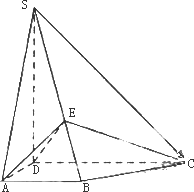
    (Ⅰ)证明：SE＝2EB；

    (Ⅱ)求二面角A－DC－C的大小．

    查看答案和解析>>

    科目：高中数学 来源：江苏省某重点中学2012届高三上学期11月练习数学试题 题型：044

    如图，四棱锥S－ABCD中，M是SB的中点，AB∥CD，BC⊥CD，且AB＝BC＝2，CD＝SD＝1，又SD⊥面SAB．

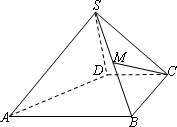
    (1)证明：CD⊥SD；

    (2)证明：CM⊥面SAD；

    (3)求四棱锥S－ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源：2011年普通高等学校招生全国统一考试全国卷数学文科 题型：044

    如图，四棱锥S－ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形．AB＝BC＝2，CD＝SD＝1．

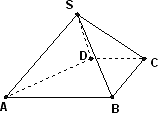
    (Ⅰ)证明：SD⊥平面SAB

    (Ⅱ)求AB与平面SBC所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源：山东省郓城一中2012届高三上学期寒假作业数学理科试卷(3) 题型：044

    如图，四棱锥S－ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB＝BC＝2，CD＝SD＝1．

    (Ⅰ)证明：SD⊥平面SAB；

    (Ⅱ)求AB与平面SBC所成角的大小．

    查看答案和解析>>

    同步练习册答案