
【题目】如表中数表为“森德拉姆筛”,其特点是每行每列都成等差数列,记第i行,第j列的数为aij,则数字41在表中出现的次数为( )
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
A.4B.8C.9D.12
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】如图,在三梭柱ABC-A1B1C1中,AC=BC,E,F分别为AB,A1B1的中点.
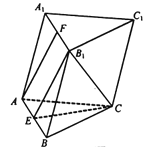
(1)求证:AF∥平面B1CE;
(2)若A1B1⊥![]() ,求证:平面B1CE⊥平面ABC.
,求证:平面B1CE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式m-|x-2|≥1,其解集为[0,4].
(1)求m的值;
(2)若a,b均为正实数,且满足a+b=m,求a2+b2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1,F2分别为椭圆![]() 的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为
的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为![]() ,且△PF1F2的最大面积为1.
,且△PF1F2的最大面积为1.
(Ⅰ)求椭圆C的方程.
(Ⅱ)点M的坐标为![]() ,过点F2且斜率为k的直线L与椭圆C相交于A,B两点.对于任意的
,过点F2且斜率为k的直线L与椭圆C相交于A,B两点.对于任意的![]() 是否为定值?若是求出这个定值;若不是说明理由.
是否为定值?若是求出这个定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),其准线方程
),其准线方程![]() ,直线
,直线![]() 过点
过点![]() (
(![]() ),且与抛物线交于
),且与抛物线交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求抛物线方程,并注明:![]() 的值与直线
的值与直线![]() 倾斜角的大小无关;
倾斜角的大小无关;
(2)若![]() 为抛物线上的动点,记
为抛物线上的动点,记![]() 的最小值为函数
的最小值为函数![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com