
 如图,在正三棱柱ABC-A1B1C1中,AB=2,AAl=3,点D为C1B的中点,点P为AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AAl=3,点D为C1B的中点,点P为AB的中点.分析 (1)连结DP,AC1,推导出DP∥AC1,由此能证明DP∥平面ACClAl•
(2)三棱锥C1-ABC的体积${V}_{{C}_{1}-ABC}$=$\frac{1}{3}×C{C}_{1}×{S}_{△ABC}$,由此能求出结果.
解答 证明:(1)连结DP,AC1,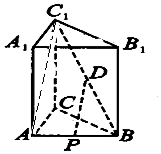
∵点D为C1B的中点,点P为AB的中点,
∴DP∥AC1,
∵DP?平面ACClAl,AC1?平面ACClAl,
∴DP∥平面ACClAl•
解:(2)∵正三棱柱ABC-A1B1C1中,AB=2,AAl=3,
∴三棱锥C1-ABC的体积:
${V}_{{C}_{1}-ABC}$=$\frac{1}{3}×C{C}_{1}×{S}_{△ABC}$=$\frac{1}{3}×3×(\frac{1}{2}×2×2×sin60°)$=$\sqrt{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
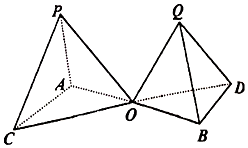 如图所示的“相邻塔”形立体建筑,已知P-OAC和Q-OBD是边长分别为a和$\frac{m}{a}({m是常数})$的两个正四面体,底面中AB与CD交于点O,试求出塔尖P,Q之间的距离关于边长a的函数,并求出a为多少时,塔尖P,Q之间的距离最短.
如图所示的“相邻塔”形立体建筑,已知P-OAC和Q-OBD是边长分别为a和$\frac{m}{a}({m是常数})$的两个正四面体,底面中AB与CD交于点O,试求出塔尖P,Q之间的距离关于边长a的函数,并求出a为多少时,塔尖P,Q之间的距离最短.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\frac{28}{3}$ | C. | $\frac{32}{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
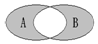 如图所示,A、B是两个非空集合,定义A*B表示阴影部分集合,若集合A={x|y=$\sqrt{3x-{x^2}}$,x,y∈R},B={y|y=2x,x>0},则A*B=( )
如图所示,A、B是两个非空集合,定义A*B表示阴影部分集合,若集合A={x|y=$\sqrt{3x-{x^2}}$,x,y∈R},B={y|y=2x,x>0},则A*B=( )| A. | [0,+∞) | B. | [0,1]∪(3,+∞) | C. | [0,1)∪[3,+∞) | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞\;,\;-\frac{2}{3}}]$ | B. | $[{\frac{2}{3}\;,\;+∞})$ | C. | $({-∞\;,\;-\frac{1}{2}}]$ | D. | $({-∞\;,\;\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.72.5>1.73 | B. | 0.6-1>0.62 | C. | 1.70.3<0.93.1 | D. | 0.8-0.1>1.250.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com