
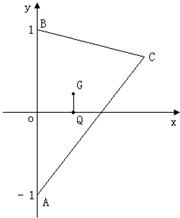
 设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.
设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.| x |
| 3 |
| y |
| 3 |
| x |
| 3 |
| x2 |
| 3 |
| x2 |
| 3 |
| x1+x2 |
| 2 |
| -3mk |
| 1+3k2 |
| (1+3k2)2 |
| 3k2 |
| 6k2-1 |
| 3k2 |
| ||
| 6 |
| ||
| 6 |
| ||
| 6 |
| ||
| 6 |


科目:高中数学 来源: 题型:
| OP |
| OQ |
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2008年广东地区数学科全国各地模拟试题直线与圆锥曲线大题集 题型:044
设G,Q分别为△ABC的重心和外心,A(0,-1),B(0,1),且GQ∥AB.
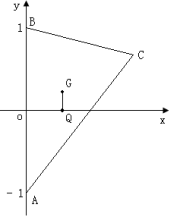
(Ⅰ)求点C的轨迹E的方程;
(Ⅱ)若l0是过点P(1,0)且垂直于x轴的直线,是否存在直线l,使得l与曲线E交于两个不同的点M,N,且MN恰被l0平分?若存在,求出l的斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
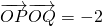 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.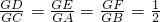 .
.查看答案和解析>>
科目:高中数学 来源:2007年江苏省盐城市滨海中学高考数学最后一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com