
���� �����к���������˵���ٴ���ֵ��֤�ڴ������ú�����ͼ��ƽ��˵������ȷ������˵���ܴ���ͼ��������ȷ��
���  �⣺��y=tan x���䶨�����ڲ������������������������䣬�ʢٴ���
�⣺��y=tan x���䶨�����ڲ������������������������䣬�ʢٴ���
�ڵ�x=$\frac{��}{12}$ʱ������$y=2sin��2x+\frac{��}{3}��$�ĺ���ֵΪ$2sin��2��\frac{��}{12}+\frac{��}{3}��=2$��
��$y=2sin��2x+\frac{��}{3}��$��ͼ���ڵ�$��\frac{��}{12}��0��$�Գƣ��ʢڴ���
�۰Ѻ���$y=3sin��{2x+\frac{��}{3}}��$��ͼ������ƽ��$\frac{��}{6}$����λ���ȵõ�����
y=3sin[2��x$-\frac{��}{6}$��+$\frac{��}{3}$]=3sin2x��ͼ�ʢ���ȷ��
�����������ǵ�һ���Ľǣ��Ҧ����£���sin����sin�£��������=330�㣬
��=60�㣻
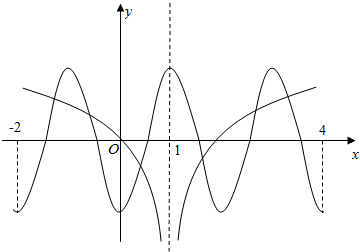
����������y=ln|x-1|��ͼ���뺯��y=-2os��x��-2��x��4����ͼ����ͼ��
��������ͼ����6�����㣬�ҹ���ֱ��x=1�Գƣ������н���ĺ�����֮�͵���6���ʢ���ȷ��
�ʴ�Ϊ���ۢݣ�
���� ���⿼�����������ж���Ӧ�ã����������Ǻ�����ͼ������ʣ��ر��Ƕ��ڢݵ��жϣ���ͼʹ�����ø���ֱ���������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������X���ϵ���Բ | B�� | ������Y���ϵ���Բ | ||
| C�� | ������X���ϵ�˫���� | D�� | ������Y���ϵ�˫���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | $\sqrt{2}$-1 | C�� | $\sqrt{2}$+1 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
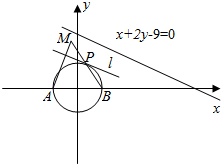 ��֪ԲC��x2+y2=1��x�����������ֱ�ΪA��B�������ң���PΪC�ϵĶ��㣬l����P����C���У�����A��l�Ĵ�������ֱ��BP���ڵ�M�����M��ֱ��x+2y-9=0�ľ�������ֵ��$2\sqrt{5}+2$��
��֪ԲC��x2+y2=1��x�����������ֱ�ΪA��B�������ң���PΪC�ϵĶ��㣬l����P����C���У�����A��l�Ĵ�������ֱ��BP���ڵ�M�����M��ֱ��x+2y-9=0�ľ�������ֵ��$2\sqrt{5}+2$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����x2+y2=0����x��yȫΪ0���ķ������������� | |
| B�� | ����f��x��=ex+x-2��������������ǣ�1��2�� | |
| C�� | ���⡰��x2-3x+2=0����x=1�����������Ϊ������x��1��x2-3x+2��0�� | |
| D�� | ��������p��?x��R��ʹ��x2+x+1��0����Vp��?x��R������x2+x+1��0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com