
【题目】设![]() ,
,![]() ,以
,以![]() 表示不是
表示不是![]() 的因数的最小自然数,例如
的因数的最小自然数,例如![]() .若
.若![]() ,又可作
,又可作![]() 等等.如果
等等.如果![]() ,那么
,那么![]() 叫做
叫做![]() 的长度.对一切
的长度.对一切![]() ,
,![]() ,用列举法表示
,用列举法表示![]() 的长度构成的集合是______.
的长度构成的集合是______.
【答案】![]()
【解析】
记![]() 的长度为Ln.
的长度为Ln.
很明显,若奇数n≥3,那么f(n)=2,因此只须讨论n为偶数的情况,
我们首先证明,对任何n≥3,f(n)=ps,这里P是素数,s为正整数.
假若不然,若f(n)有两个不同的素因子,这时总可以将f(n)表为f(n)=ab,其中a、b是大于1的互素的正整数.
由f的定义知,a与b都应能整除n,因(a,b)=1,故ab也应整除n,这与f(n)=ab矛盾.
所以f(n)=ps.
由此可以得出以下结论:
(1)当n为大于1的奇数时,f(n)=2,故Ln=1;
(2)设n为大于2的偶数,如果f(n)=奇数,那么f(f(n))=2,这时Ln=2;
如果f(n)=2s,其中自然数s≥2,那么f(f(n))=f(2s)=3,从而f(f(f(n)))=f(3)=2,这时Ln=3.
综上可得,用列举法表示![]() 的长度构成的集合是
的长度构成的集合是![]() .
.


科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的。在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点![]() 定义它们之间的一种“距离”:
定义它们之间的一种“距离”:![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]() 上一点
上一点![]() 到点
到点![]() 的“距离”;
的“距离”;
(2)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆”上的所有点到点![]() 的“距离”均为
的“距离”均为![]() 的“圆”方程,并求该“圆”围成的图形的面积;
的“圆”方程,并求该“圆”围成的图形的面积;
(3)若点![]() 到点
到点![]() 的“距离”和点
的“距离”和点![]() 到点
到点![]() 的“距离”相等,其中实数
的“距离”相等,其中实数![]() 满足
满足![]() ,求所有满足条件的点
,求所有满足条件的点![]() 的轨迹的长之和.
的轨迹的长之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点![]() 是抛物线
是抛物线![]() 上一定点,直线
上一定点,直线![]() 的倾斜角互补,且与抛物线另交于
的倾斜角互补,且与抛物线另交于![]() ,
,![]() 两个不同的点.
两个不同的点.
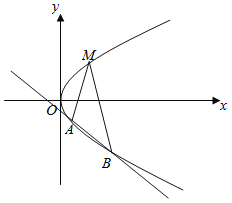
(1)求点![]() 到其准线的距离;
到其准线的距离;
(2)求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 上的动点,当
上的动点,当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲所示,![]() 是梯形
是梯形![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,先将梯形
,先将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() .
.
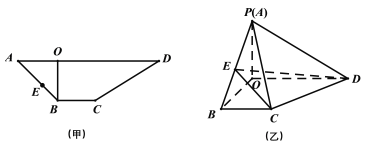
(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)点![]() 是线段
是线段![]() 上一动点,当直线
上一动点,当直线![]() 与
与![]() 所成的角最小时,求二面角
所成的角最小时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() ,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积与上一年剩余面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com