
分析 (1)表示出f(x)的最小值,得到关于m的方程,解出m的值,求出函数的单调区间即可;
(2)当m=0时,经检验不满足条件.当f(x)在[0,2]上有一个零点时,求出m的值.当f(x)在[0,2]上有两个零点时,求出m的取值范围,再取并集即得所求.
解答 解:(1)f(x)的最小值是$\frac{4{-(m-1)}^{2}}{4}$=-3,解得:m=5;
故f(x)=x2+4x+1,对称轴是x=-2,
故f(x)在(-∞,-2)递减,在(-2,+∞)递增;
(2)当m=0时,函数f(x)=x2-x+1,在区间[0,2]上没有零点,不满足条件,故舍去.
当f(x)在[0,2]上有一个零点时,此时①$\left\{\begin{array}{l}{△{=(m-1)}^{2}-4=0}\\{0≤-\frac{m-1}{2}≤2}\end{array}\right.$,或 ②$\left\{\begin{array}{l}{△{=(m-1)}^{2}-4>0}\\{f(0)•f(2)<0}\end{array}\right.$成立,
解①得 m=-1,解②得 m<-$\frac{3}{2}$,
当f(x)在[0,2]上有两个零点时,此时 $\left\{\begin{array}{l}{△{=(m-1)}^{2}-4>0}\\{0≤-\frac{m-1}{2}≤2}\\{f(0)≥0}\\{f(2)≥0}\end{array}\right.$,解得-$\frac{3}{2}$≤m<-1,
综上可得,实数m的取值范围[-∞,-1].
点评 本题考查二次函数与方程之间的关系,二次函数在给定区间上的零点问题,要注意函数图象与x轴相切的情况,属于中档题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:解答题
已知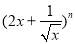 的展开式前两项的二项式系数之和为10.
的展开式前两项的二项式系数之和为10.
(1)求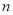 的值.
的值.
(2)求出这个展开式中的常数项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3\sqrt{3}}{2}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{3\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{8}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
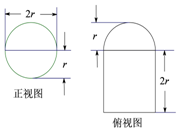 圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )| A. | 32+80π | B. | 64+40$\sqrt{2}$π | C. | 64+80π | D. | 100+125π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com