
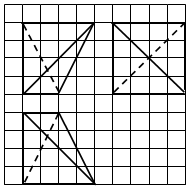
 如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为( )| A. | 2$\sqrt{2}$ | B. | $\frac{7\sqrt{2}}{3}$ | C. | $\sqrt{11}$ | D. | 2$\sqrt{3}$ |
分析 根据三视图知几何体是三棱锥为棱长为4的正方体一部分,画出直观图,由正方体的性质求出棱长、判断出各面形状,画出三棱锥C-ABD以及外接球,由△ABD是等边三角形,判断出球心O在△ABD的射影的位置,判断线与线的位置关系,设出未知数画出平面图形,利用勾股定理列出方程组,求出该四面体的外接球半径.
解答 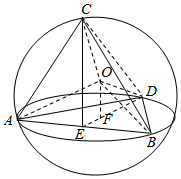 解:由三视图知几何体是三棱锥A-BCD,为棱长为4的正方体一部分,
解:由三视图知几何体是三棱锥A-BCD,为棱长为4的正方体一部分,
直观图如图所示: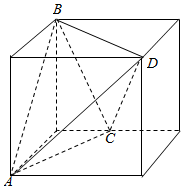
由正方体的性质可得,AB=AD=BD=4$\sqrt{2}$,
AC=BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,CD=$\sqrt{{2}^{2}+{4}^{2}+{4}^{2}}$=6,
设三棱锥C-ABD的外接球球心是O,设半径是R,
取AB的中点E,连接CE、DE,如图所示:
设OA=OB=OC=OD=R,△ABD是等边三角形,
∴O在底面△ABD的射影是△ABD中心F,
∵DE⊥BE,BE=2$\sqrt{2}$,∴DE=$\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}$=$2\sqrt{6}$,
同理可得,CE=$2\sqrt{3}$,则满足CE2+DE2=CD2,即CE⊥DE,
在RT△CED中,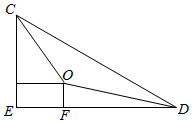 设OF=x,
设OF=x,
∵F是等边△ABD的中心,
∴$DF=\frac{2}{3}DE=\frac{4\sqrt{6}}{3}$,
$EF=\frac{1}{3}DE=\frac{2\sqrt{6}}{3}$,
则$\left\{\begin{array}{l}{O{D}^{2}=O{F}^{2}+D{F}^{2}}\\{O{C}^{2}=E{F}^{2}+(CE-OF)^{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{R}^{2}={x}^{2}+{(\frac{4\sqrt{6}}{3})}^{2}}\\{{R}^{2}={(\frac{2\sqrt{6}}{3})}^{2}+{(2\sqrt{3}-x)}^{2}}\end{array}\right.$,解得x=$\frac{\sqrt{3}}{3}$,
代入其中一个方程得,R=$\sqrt{(\frac{\sqrt{3}}{3})^{2}+(\frac{4\sqrt{6}}{3})^{2}}$=$\sqrt{\frac{99}{9}}$=$\sqrt{11}$,
∴该四面体的外接球半径是$\sqrt{11}$,
故选:C.
点评 本题考查由三视图求几何体外接球的表面积,以及三棱锥外接球问题,在三视图与直观图转化过程中,以一个正方体为载体是很好的方式,使得作图更直观,考查空间想象能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
若集合 满足
满足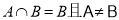 ,则命题“
,则命题“ ”是命题“
”是命题“ ”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{3}{2}$) | C. | ($\frac{1}{2}$,$\frac{5}{2}$) | D. | ($\frac{3}{2}$,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,CC1=2,点P是侧棱C1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,CC1=2,点P是侧棱C1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
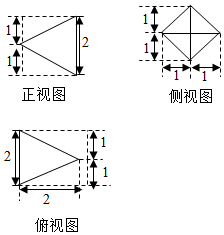 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3>b3 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | lga>lgb | D. | $\sqrt{a}$>$\sqrt{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com