已知四面体的4条棱的长为2,2条棱的长为3,求它的体积.
【答案】
分析:由给出的四面体的4条棱的长为2,2条棱的长为3,分两类情况作出图形,经求解可知,当两条长为3的棱异面时,四面体不存在,当两条长为3的棱共面时,把要求的四面体的体积转化为两个三棱锥的体积和,求出共同的底面积后代入棱锥体积公式求解.
解答:
解:根据分析可知满足题目条件的四面体有两种情况,也就是棱长为3的棱共面和异面
(1)当棱长为3的棱异面时,四面体的图形如左图,
取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD.
则
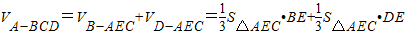
=
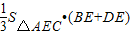
=

在直角三角形AEB和直角三角形CEB中,求得
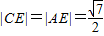
,
∵|CE|+|AE|=

<3=|AC|,所以三角形AEC并不存在,即这种情况的三棱锥也不存在.
(2)当棱长为3的棱共面时,四面体的图形如右图,
取BC中点E,则AE⊥BC,DE⊥BC,
则

=
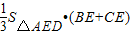
=

在三角形AED中,AE=

,DE=

,AD=2,
所以

=

.
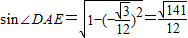
.
所以

=

.
所以,
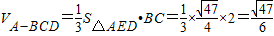
.
点评:本题考查了棱锥的体积,考查了分类讨论的数学思想和数学转化思想,能够正确排除两条长为3的棱异面时的情况是解答该题的关键.此题是中档题

 解:根据分析可知满足题目条件的四面体有两种情况,也就是棱长为3的棱共面和异面
解:根据分析可知满足题目条件的四面体有两种情况,也就是棱长为3的棱共面和异面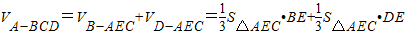
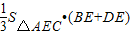 =
=
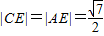 ,
, <3=|AC|,所以三角形AEC并不存在,即这种情况的三棱锥也不存在.
<3=|AC|,所以三角形AEC并不存在,即这种情况的三棱锥也不存在.
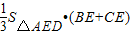 =
=
 ,DE=
,DE= ,AD=2,
,AD=2, =
= .
.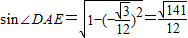 .
. =
= .
.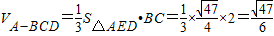 .
.
