
【题目】在平面直角坐标系中,已知曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 分别作射线
分别作射线![]() 、
、![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,且
,且![]() .试探究直线
.试探究直线![]() 是否过定点?如果是,请求出该定点;如果不是,请说明理由
是否过定点?如果是,请求出该定点;如果不是,请说明理由
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=![]() (弦矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
(弦矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长等于9米的弧田.
,弦长等于9米的弧田.

(1)计算弧田的实际面积;
(2)按照《九章算术》中弧田面积的经验公式计算所得结果与(1)中计算的弧田实际面积相差多少平方米?(结果保留两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在正常数
,若存在正常数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,则称
均成立,则称![]() 是“控制增长函数”。在以下四个函数中:①
是“控制增长函数”。在以下四个函数中:①![]() ②
②![]() ③
③![]() ④
④![]() 是“控制增长函数”的有(空格上填入函数代码)________.
是“控制增长函数”的有(空格上填入函数代码)________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,给出下列四个命题:
,给出下列四个命题:
①若![]() 是偶函数,则
是偶函数,则![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
②若![]() ,则
,则![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③若![]() ,且
,且![]() ,则
,则![]() 的一个周期为2;
的一个周期为2;
④![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
其中正确命题的序号为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4,0)、B(1,0),动点M满足|AM|=2|BM|.
(1)求动点M的轨迹C的方程;
(2)直线l:x+y=4,点N∈l,过N作轨迹C的切线,切点为T,求NT取最小时的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当函数的自变量取值区间与值域区间相同时,我们称这样的区间为该函数的保值区间,函数的保值区间有![]() 、
、![]() 、
、![]() 三种形式,以下四个二次函数图像的对称轴是直线
三种形式,以下四个二次函数图像的对称轴是直线![]() ,从图像可知,有二个保值区间的函数是( )
,从图像可知,有二个保值区间的函数是( )
A.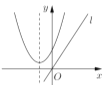 B.
B. C.
C.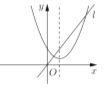 D.
D.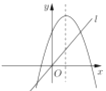
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com