
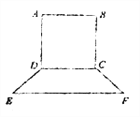
【题目】要制作一个如图的框架(单位:米).要求所围成的总面积为19.5(![]() ),其中
),其中![]() 是一个矩形,
是一个矩形, ![]() 是一个等腰梯形,梯形高
是一个等腰梯形,梯形高![]() ,
, ![]() ,设
,设![]() 米,
米, ![]() 米.
米.
(1)求![]() 关于
关于![]() 的表达式;
的表达式;
(2)如何设计![]() ,
,![]() 的长度,才能使所用材料最少?
的长度,才能使所用材料最少?
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 君不小于25”的概率;
君不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5填中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程,
的线性回归方程,![]() .
.
(参考公式: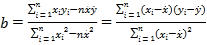 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 的直角坐标方程以及直线
的直角坐标方程以及直线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于两点,求
交于两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电动摩托车的续航里程,是指电动摩托车在蓄电池满电量的情况下一次能行驶的最大距离.为了解A,B两个不同型号电动摩托车的续航里程,现从某卖场库存电动摩托车中随机抽取A,B两个型号的电动摩托车各5台,在相同条件下进行测试,统计结果如下:
电动摩托车编号 | 1 | 2 | 3 | 4 | 5 |
A型续航里程(km) | 120 | 125 | 122 | 124 | 124 |
B型续航里程(km) | 118 | 123 | 127 | 120 | a |
已知A,B两个型号被测试电动摩托车续航里程的平均值相等.
(1)求a的值;
(2)求A型号被测试电动摩托车续航里程标准差的大小;
(3)从被测试的电动摩托车中随机抽取A,B型号电动摩托车各1台,求至少有1台的续航里程超过122km的概率.
(注:n个数据![]() ,的方差
,的方差![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 到抛物线C:y2=2px
到抛物线C:y2=2px![]() 准线的距离为2.
准线的距离为2.
(Ⅰ)求C的方程及焦点F的坐标;
(Ⅱ)设点P关于原点O的对称点为点Q,过点Q作不经过点O的直线与C交于两点A,B,直线PA,PB,分别交x轴于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要从甲、乙两名同学中选择一人参加该市组织的数学竞赛,已知甲、乙两名同学最近7次模拟竞赛的数学成绩(满分100分)如下:
甲:79,81,83,84,85,90,93;
乙:75,78,82,84,90,92,94.
(1)完成答题卡中的茎叶图;
(2)分别计算甲、乙两名同学最近7次模拟竞赛成绩的平均数与方差,并由此判断该校应选择哪位同学参加该市组织的数学竞赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com