
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了![]() 名女性或
名女性或![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
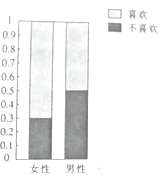
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
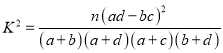 ,其中
,其中![]()
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
A小区 | 低碳族 | 非低碳族 |
比例 |
|
|
B小区 | 低碳族 | 非低碳族 |
比例 |
|
|
C小区 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)从A,B,C三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将数列
,则将数列![]() 和
和![]() 的距离定义为
的距离定义为![]() .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,数列
的集合,数列![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() .若
.若![]() ,
, ![]() ,数列
,数列![]() 和
和![]() 的距离小于2016,求
的距离小于2016,求![]() 的最大值.
的最大值.
(3)记![]() 是所有7项数列
是所有7项数列![]() (其中
(其中![]() ,
, ![]() 或
或![]() )的集合,
)的集合, ![]() ,且
,且![]() 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: ![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).以原点
).以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从![]() 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到
两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到![]() 地区用户满意度评分的频率分布直方图和
地区用户满意度评分的频率分布直方图和![]() 地区用户满意度评分的频数分布表.
地区用户满意度评分的频数分布表.
![]() 地区用户满意度评分的频率分布直方图
地区用户满意度评分的频率分布直方图
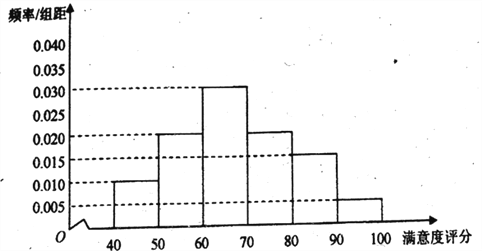
![]() 地区用户满意度评分的频数分布表
地区用户满意度评分的频数分布表
满意度评分分组 |
|
|
|
|
|
频数 | 2 | 8 | 14 | 10 | 6 |
(1)在答题卡上作出![]() 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:

估计哪个地区的满意度等级为不满意的概率大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,给出四个结论:
,给出四个结论:
①函数![]() 是最小正周期为
是最小正周期为![]() 的奇函数;
的奇函数;
②函数![]() 的图像的一条对称轴是
的图像的一条对称轴是![]() ;
;
③函数![]() 图像的一个对称中心是
图像的一个对称中心是![]() ;
;
④函数![]() 的递增区间为
的递增区间为![]() .则正确结论的个数为( )
.则正确结论的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(![]() ,表示丢失的数据)
,表示丢失的数据)
无意愿 | 有意愿 | 总计 | |
男 |
|
| 40 |
女 | 5 |
|
|
总计 | 25 |
| 80 |
(1)求出![]() 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
(2)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据: 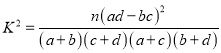 ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com