
【题目】用二分法求![]() 的近似值(精确度0.1).
的近似值(精确度0.1).
【答案】2.25
【解析】试题分析:令f(x)=x2-5,由零点存在性定理得f(2.2)·f(2.4)<0,函数在区间(2.2,2.4)内有零点x0再由f(2.2)·f(2.3)<0,所以x0∈(2.2,2.3),依次进行到区间长度为0.1时即可.
试题解析:
设x=![]() ,则x2=5,即x2-5=0,
,则x2=5,即x2-5=0,
令f(x)=x2-5.
因为f(2.2)=-0.16<0,f(2.4)=0.76>0,
所以f(2.2)·f(2.4)<0,
说明这个函数在区间(2.2,2.4)内有零点x0,
取区间(2.2,2.4)的中点x1=2.3,则f(2.3)=0.29.
因为f(2.2)·f(2.3)<0,所以x0∈(2.2,2.3),
再取区间(2.2,2.3)的中点
x2=2.25,f(2.25)=0.062 5.
因为f(2.2)·f(2.25)<0,
所以x0∈(2.2,2.25).由于|2.25-2.2|=0.05<0.1,所以![]() 的近似值可取为2.25.
的近似值可取为2.25.


科目:高中数学 来源: 题型:
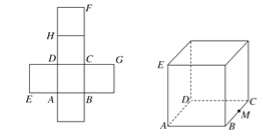
【题目】【2017银川一中高考模拟文】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台. 现销售给A地10台,B地8台. 已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9 000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
频数 | 35 | 20 | 25 | 20 |
支持脱欧的人数 | 10 | 10 | 15 | 15 |
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持“脱欧”人数 | |||
不支持“脱欧”人数 | |||
合计 |
附:![]()

(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com