
【题目】已知数列![]() 中,
中,![]() ,对任意的
,对任意的![]() ,
,![]() ,有
,有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() (
(![]() ,
,![]() ),
),
①求数列![]() 的前
的前![]() 项和
项和![]() ;
;
②设![]() 是正整数,若存在正数
是正整数,若存在正数![]() ,对任意的正整数
,对任意的正整数![]() ,当
,当![]() 时,都有
时,都有![]() ,求m的最大值.
,求m的最大值.
【答案】(1)![]() (2)答案不唯一,具体见解析(3)
(2)答案不唯一,具体见解析(3)![]() 的最大值为5
的最大值为5
【解析】
(1)先证明![]() 是首项,公差都为1的等差数列,再写出数列的通项;(2)①先求出
是首项,公差都为1的等差数列,再写出数列的通项;(2)①先求出![]() ,(
,(![]() ),再分类讨论求出数列
),再分类讨论求出数列![]() 的前
的前![]() 项和
项和![]() ;②原题等价于存在正数
;②原题等价于存在正数![]() ,对任意的正整数
,对任意的正整数![]() (
(![]() ),当
),当![]() 时,都有
时,都有![]() ,再对
,再对![]() 分类讨论求出m的最大值.
分类讨论求出m的最大值.
(1)由![]() ,
,![]() ,令
,令![]() ,
,
则![]() ,所以
,所以![]() 是首项,公差都为1的等差数列,
是首项,公差都为1的等差数列,
所以![]() 的通项公式为
的通项公式为![]() .
.
(2)由题意![]() ,
,
![]() (
(![]() ),
),
两式相减得![]() (
(![]() ),
),![]() ,(
,(![]() ),
),
当![]() 时,
时,![]() 满足上式,所以
满足上式,所以![]() ,(
,(![]() ).
).
所以①![]() 时,
时,![]() ,
,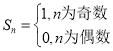 ;
;
②![]() 时,
时,![]() ,
,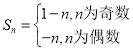
③![]() 且
且![]() 时,
时,![]() ,
,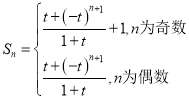 .
.
(3)![]() 等价于
等价于![]() ,
,![]() ,
,
原题等价于存在正数![]() ,对任意的正整数
,对任意的正整数![]() (
(![]() ),当
),当![]() 时,都有
时,都有![]() ,
,
①当![]() 时,
时,![]() ,与题目要求不符;
,与题目要求不符;
②当![]() 时,
时,![]() ,与题目要求不符;
,与题目要求不符;
③当![]() 时,当
时,当![]() 时,上式取对数得
时,上式取对数得![]() ,
,
等价于![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() 单调递增;
单调递增;
![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
所以![]() 在
在![]() 取最大值,
取最大值,
又因为![]() ,所以
,所以![]() ;
;
设![]() ,
,![]() ,则
,则 ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() 时
时![]() ,所以
,所以![]() 在
在![]() 递减,
递减,
又![]() ,所以
,所以![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 递减.
递减.
![]() 时,
时,![]() ,
,![]() 存在;
存在;
![]() 时,
时,![]() ,
,![]() 递减,
递减,
![]() ,
,![]() ,
,
所以![]() 的最大值为5.
的最大值为5.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】第十一届全国少数民族传统体育运动会在河南郑州举行,某项目比赛期间需要安排3名志愿者完成5项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式共有多少种
A.60B.90C.120D.150
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水箱用的“浮球”是由两个相同半球和一个圆柱筒组成,它的轴截面如图所示,已知半球的直径是![]() ,圆柱筒高
,圆柱筒高![]() ,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆
,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 及
及![]() 焊接而成,其中
焊接而成,其中![]() ,
,![]() 分别是圆柱上下底面的圆心,
分别是圆柱上下底面的圆心,![]() ,
,![]() ,
,![]() ,
,![]() 均在“浮球”的内壁上,AC,BD通过“浮球”中心
均在“浮球”的内壁上,AC,BD通过“浮球”中心![]() ,且
,且![]() 、
、![]() 均与圆柱的底面垂直.
均与圆柱的底面垂直.
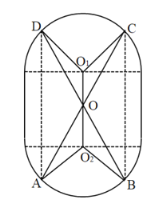
(1)设![]() 与圆柱底面所成的角为
与圆柱底面所成的角为![]() ,试用
,试用![]() 表示出防压卡中四边形
表示出防压卡中四边形![]() 的面积
的面积![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)研究表明,四边形![]() 的面积越大,“浮球”防压性越强,求四边形
的面积越大,“浮球”防压性越强,求四边形![]() 面积取最大值时,点
面积取最大值时,点![]() 到圆柱上底面的距离
到圆柱上底面的距离![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面ABCD平面PAD,
中,平面ABCD平面PAD,![]() ,
,![]() ,
,![]() ,
,![]() ,E是PD的中点.
,E是PD的中点.

![]() 证明:
证明:![]() ;
;
![]() 设
设![]() ,点M在线段PC上且异面直线BM与CE所成角的余弦值为
,点M在线段PC上且异面直线BM与CE所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
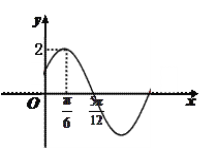
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(2)①当![]() ,
,![]() 时,若对于任意
时,若对于任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;②当
的最小值;②当![]() 时,设函数
时,设函数![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程
的参数方程![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com