练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是　　　　.

     

     

    【答案】

    32π

    【解析】法一　设球的半径与圆柱的高所成的角为α,

    则圆柱底面半径为4sinα,高为8cosα,

    ∴S圆柱侧=2π·4sinα·8cosα=32πsin2α.

    当sin2α=1时,S圆柱侧最大为32π.

    此时S球表-S圆柱侧=4π·42-32π=32π.

    法二　设圆柱底面半径为r,则其高为2,

    ∴S圆柱侧=2πr·2=4π≤

    4π=2πR2

    （“=”）.

    又R=4,∴S圆柱侧最大为32π.

    此时S球表-S圆柱侧=4π·42-32π=32π.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：数学教研室 题型：044

    如图所示，扇形AOB的弧的长是半径的2倍，弦AB的长为4，求的长度及扇形AOB的面积．

     

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修2－2)　2009－2010学年　第27期　总第183期 北师大课标 题型：022

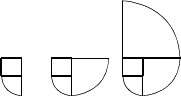
    如图所示，小正方形的边长为1，渐开线形成的螺旋曲线是由半径分别为1，2，3，4，…，n的四分之一圆弧逆时针形成的螺线图案，并且分别以正方形的各个顶点为圆心，则第n个图形的圆弧长度的通项公式为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    选修4－1：几何证明选讲如图所示，为⊙的直径，、为⊙的切线，、为切点(1)求证：(2)若⊙的半径为，求AD·OC的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    修建一储粮仓库,形状如图所示,底部为圆柱形,顶部为半球 形, 仓库侧面的每平方米造价是底面每平方米造价的4倍,顶部的每平方米造价是底面每平方米造价的5.5倍, 已知仓库底面的每平方米造价为15元,若修建仓库的总费用为9万元, 问仓库底面半径为多少米时,仓库的容积最大, 最大容积是多少(π取3计算)?

    查看答案和解析>>

    同步练习册答案