
【题目】己知点A是抛物线![]() 的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足
的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足![]() ,当
,当![]() 取最大值时,点P恰好在以A、B为焦点的双曲线上,则双曲线的离心率为
取最大值时,点P恰好在以A、B为焦点的双曲线上,则双曲线的离心率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】一个盒子中装有标号为1,2,3,4,5的5张标签,随机地依次选取两张标签,根据下列条件求两张标签上的数字为相等整数的概率;
(1)标签的选取是不放回的;
(2)标签的选取是有放回的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:x2=2py (p>0) 的焦点,点A(m,3)在抛物线C上,且|AF|=5,若点P是抛物线C上的一个动点,设点P到直线![]() 的距离为
的距离为![]() ,设点P到直线
,设点P到直线![]() 的距离为
的距离为![]() .
.
(1)求抛物线C的方程;
(2) 求![]() 的最小值;
的最小值;
(3)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: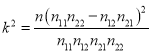 ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内点![]() 到点
到点![]() 的距离和到直线
的距离和到直线![]() 的距离之比为
的距离之比为![]() ,若动点P的轨迹为曲线C.
,若动点P的轨迹为曲线C.
(I)求曲线C的方程;
(II)过F的直线![]() 与C交于A,B两点,点M的坐标为
与C交于A,B两点,点M的坐标为![]() 设O为坐标原点.证明:
设O为坐标原点.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: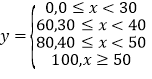 ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
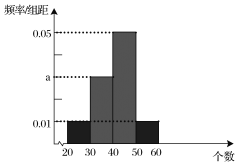
(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() .沿
.沿![]() 将△
将△![]() 翻折到△
翻折到△![]() ,连接
,连接![]() ,得到如图的五棱锥
,得到如图的五棱锥![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com