在三角形ABC中，已知
，解三角形ABC。
科目：高中数学 来源： 题型：解答题
风景秀美的京娘湖畔有四棵高大的银杏树，记做
、
、
、
，欲测量、两棵树和、两棵树之间的距离，但湖岸部分地方围有铁丝网不能靠近，现在可以方便的测得、两点间的距离为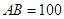
米，如图，同时也能测量出
，
，
，
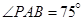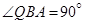，则、两棵树和、两棵树之间的距离各为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
如图，A，B，C三个观察哨，A在B的正南，两地相距6km，C在B的北偏东60°，两地相距4km.在某一时刻，A观察哨发现某种信号，并知道该信号的传播速度为1km/s；4秒后B,C两个观察哨同时发现这种信号．在以过A,B两点的直线为y轴，以线段AB的垂直平分线为x轴的平面直角坐标系中，试求出发了这种信号的地点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，故角C为30度，则根据内角和定理可知A为90度，然后再有正弦定理可知
中，
的对边分别为
，且
． 
的值；
，
，求
和
．
的三个内角
、
、
的对边分别为
、
、
，且
．
的值；
，求
中，角
所对的边分别为
，满足
．
；
的取值范围．
中，
分别是角A、B、C的对边，且满足：
．
的单调减区间和取值范围．
是三角形的内角，且
和
是关于
方程
的两个根.
的值； （2）求
的值. 
中，已知
，
，设
，
.
为何值时