练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

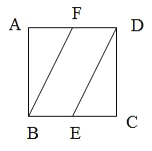
    【题目】如图，在棱长为1正方体中，点，分别为边，的中点，将沿所在的直线进行翻折，将沿所在直线进行翻折，在翻折的过程中，下列说法错误的是（ ）

    A. 无论旋转到什么位置，、两点都不可能重合

    B. 存在某个位置，使得直线与直线所成的角为

    C. 存在某个位置，使得直线与直线所成的角为

    D. 存在某个位置，使得直线与直线所成的角为

    【答案】D

    【解析】

    利用圆锥的几何特征逐一判断即可.

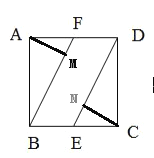
    解：过A点作AM⊥BF于M，过C作CN⊥DE于N点

    在翻折过程中，AF是以F为顶点，AM为底面半径的圆锥的母线，同理，AB，EC，DC也可以看成圆锥的母线；

    在A中，A点轨迹为圆周，C点轨迹为圆周，显然没有公共点，故A正确；

    在B中，能否使得直线AF与直线CE所成的角为60°，又AF，EC分别可看成是圆锥的母线，只需看以F为顶点，AM为底面半径的圆锥的轴截面的顶角是否大于等于60°即可，故B正确；

    在C中，能否使得直线AF与直线CE所成的角为90°，只需看以F为顶点，AM为底面半径的圆锥的轴截面的顶角是否大于等于90°即可，故C正确；

    在D中，能否使得直线与直线所成的角为，只需看以B为顶点，AM为底面半径的圆锥的轴截面的顶角是否大于等于90°即可，故D不成立；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）若，且，求的最小值；

    （2）若，且在上恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高二丈，问：积几何?”其意思为：“今有底面为矩形的屋脊状的楔体，下底面宽3丈，长4丈，上棱长2丈，高2丈，问：它的体积是多少?”已知l丈为10尺，该楔体的三视图如图所示，其中网格纸上小正方形边长为1，则该楔体的体积为（ ）

    A. 10000立方尺 B. 11000立方尺

    C. 12000立方尺 D. 13000立方尺

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若质地均匀的六面体玩具各面分别标有数字1,2,3,4,5,6．抛掷该玩具后，任何一个数字所在的面朝上的概率均相等．抛掷该玩具一次，记事件A=“向上的面标记的数字是完全平方数（即能写出整数的平方形式的数，如9=32,9是完全平方数）”

    （1）甲、乙二人利用该玩具进行游戏，并规定：①甲抛掷一次，若事件A发生，则向上一面的点数的6倍为甲的得分；若事件A不发生，则甲得0分；②乙抛掷一次，将向上的一面对应的数字作为乙的得分。现甲、乙二人各抛掷该玩具一次，分别求二人得分的期望；

    （2）抛掷该玩具一次，记事件B=“向上一面的点数不超过”，若事件A与B相互独立，试求出所有的整数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆和双曲线有共同的焦点，，点是，的交点，若是锐角三角形，则椭圆离心率的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某良种培育基地正在培育一种小麦新品种A，将其与原有的一个优良品种B进行对照试验，两种小麦各种植了24亩，所得亩产数据（单位：千克）如下：

    品种A:357，359，367，368，375，388，392，399，400，405，412，414，415，421，423，423，427，430，430，434，443，445，451，454

    品种B：363，371，374，383，385，386，391，392，394，395，397，397，400，401，401，403，406，407，410，412，415，416，422，430

    （1）画出茎叶图.

    （2）用茎叶图处理现有的数据，有什么优点？

    （3）通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在矩形中，，，是的中点，以为折痕将向上折起，变为，且平面平面.

    （Ⅰ）求证：；

    （Ⅱ）求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数,

    （1）若不等式的解集为，求的值；

    （2）若，求的最小值．

    （3）若 求不等式的解集.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形。沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥。当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为_______。

    查看答案和解析>>

    同步练习册答案