Question

【题目】如图，直三棱柱中，、分别是,的中点，.

（1）证明：∥平面；

（2）求二面角的正弦值.

Answer 1

【答案】（1）详见解析（2）

【解析】

试题分析：（Ⅰ）连接AC1交A1C于点F，由三角形中位线定理得BC1∥DF，由此能证明BC1∥平面A1CD；（Ⅱ）以C为坐标原点，的方向为x轴正方向，的方向为y轴正方向，的方向为z轴正方向，建立空间直角坐标系C-xyz．分别求出平面的法向量和平面的法向量，利用向量法能求出二面角的正弦值

试题解析：（1）证明：连接，交于点

则为的中点

又是的中点，连接

则∥，因为平面，平面

所以∥平面

（2）解：由，得

以为坐标原点，、、为轴、轴、轴建立如图的空间坐标系，

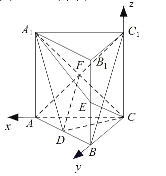
设，则，，，，，

设是平面的法向量，

则，即，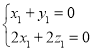

可取

同理，设是平面的法向量，则，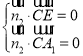

可取

从而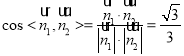

故

即二面角的正弦值为.